Lots of lines

Geometry Level 5

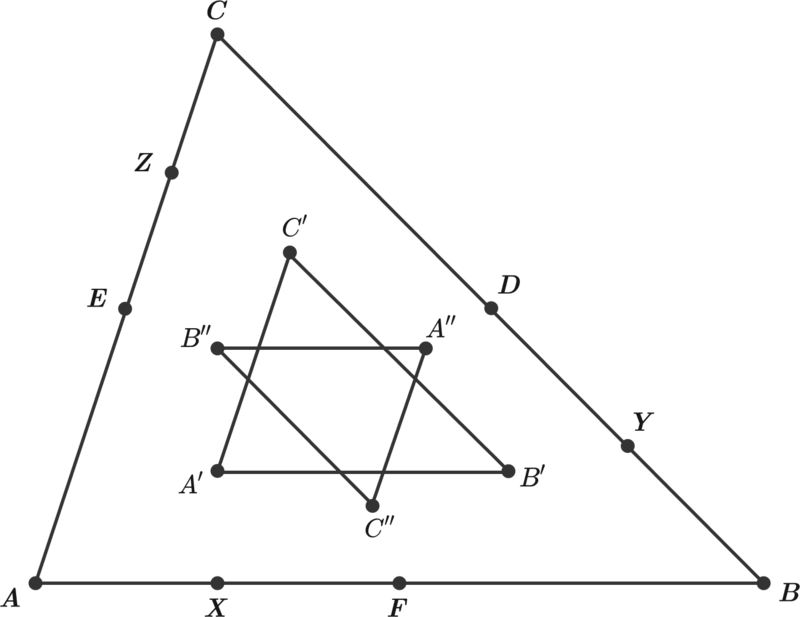
$ABC$ is a triangle. Let the midpoints of $BC$ , $CA$ , $AB$ be $D$ , $E$ , $F$ respectively. Let $X$ , $Y$ , $Z$ be the midpoints of $AF$ , $BD$ , $CE$ , respectively.

Let $A'$ be the intersections of $AD$ and $CX$ and $A''$ be the intersection of $AD$ and $BZ$ . Similarly, let $B'$ be the intersections of $BE$ and $AY$ and $B''$ be the intersection of $BE$ and $CX$ . Also, Let $C'$ be the intersections of $CF$ and $BZ$ and $C''$ be the intersection of $CF$ and $AY$ .

If the ratio of the area of $A''B''C''$ to the area of $A'B'C'$ can be represented as $\frac{p}{q}$ , where $p$ and $q$ are coprime positive integers, find $p+q$ .

The answer is 74.

2 solutions

Kelvin Hong
Feb 26, 2017

By using vector
We can get
AA'=0.4 AD
As the same ,we also get
BB'=0.4 BE
CC'=0.4 CF

Let the point that three median meet be G
We get
AG=0.667AD
As BG and CG

By using similiar triangle ,we know the fact
Area of triangle A'B'C'=(4/25) Area of triangle ABC------(1)

Using again vector ,we get
AA"=(6/7)AD
As BB",CC".
By using similiar triangle again ,we get
Area of triangle A"B"C"=(4/49)Area of triangle ABC-------(2)
By the two equations above,we get the ratio be 25/49
So the answer is
25+49=

\boxed {74}

Make sure you surround your latex with \ ( and ) \ (without the spaces). Otherwise, good solution.

Sharky Kesa - 4 years, 3 months ago

owh thanks ,I am confused about that..

Kelvin Hong - 4 years, 2 months ago

(Can also be solved even more easily and without vectors. Use Menelaus Theorem to get the required ratios. And then use similarity to express the areas of each triangle in the terms of the bigger one. Then compare them./)

Vishwash Kumar ΓΞΩ - 4 years, 3 months ago

Ya ,that Theorem also can solve this question, but I have little bit forgot about it ,I am also want to use a simpler way to solve.

Kelvin Hong - 4 years, 2 months ago

Marta Reece
Mar 7, 2017

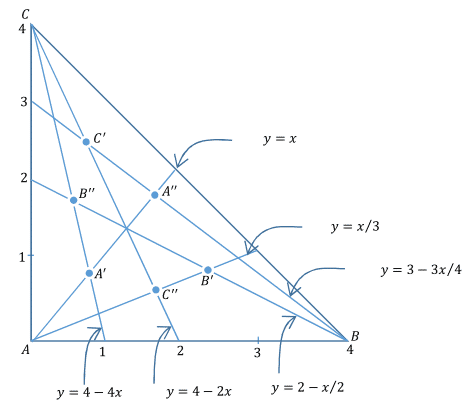
Since ratios of areas and ratios of distances on the same line are not affected by linear transformation, we can do the solution for a particular triangle. I have chosen a right isosceles triangle with legs equal 4 and placed it in a coordinate system as shown above. The equations of lines we need intersections of are also listed.

Coordinates of the points in question will then be:

$A'=(\frac{4}{5},\frac{4}{5}), B'=(\frac{12}{5},\frac{4}{5}), C'=(\frac{4}{5},\frac{12}{5})$ . Triangle $A'B'C'$ is a right triangle and its area is $\frac{1}{2}\times(\frac{8}{5})^2=\frac{32}{25}$ .

$A''=(\frac{12}{7},\frac{12}{7}), B''=(\frac{4}{7},\frac{12}{7}), C''=(\frac{12}{7},\frac{4}{7})$ . Triangle $A''B''C''$ is a right triangle and its area is $\frac{1}{2}\times(\frac{8}{7})^2=\frac{32}{49}$ .

The ratio of the areas is therefore $\frac{25}{49}$ .

Lots of lines

The answer is 74.

2 solutions

0 pending reports