lots of log

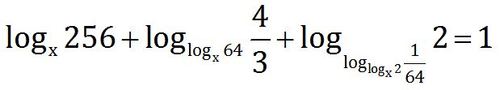
I have not been successful in obtaining a solution using only algebraic manipulations. A rewrite and a few "qualified" guesses did the job for me.

Let us rewrite the equation $\log_x 256 + \log_{\log_x 64} \frac{4}{3} + \log_{\log_{\log_x 2} \frac{1}{64}} 2 = 1$

Since $\log_x a = \frac{\log_2 a}{\log_2 x}$ , we can let $y = \log_2 x$ and get the following

$\begin{aligned} \frac{\log_2 256}{\log_2 x} + \frac{\log_2 \frac{4}{3}}{\log_2 \frac{\log_2 64}{\log_2 x}} + \frac{\log_2 2}{\log_2 \left( \frac{- \log_2 64}{\log_2 \frac{\log_2 2}{\log_2 x}} \right)} & = \\ \frac{8}{y} + \frac{\log_2 \frac{4}{3}}{\log_2 \frac{6}{y}} + \frac{1}{\log_2 \left( \frac{- 6}{\log_2 \frac{1}{y}} \right)} & = \\ \frac{8}{y} + \frac{2 - \log_2 3}{\log_2 6 - \log_2 y} + \frac{1}{\log_2 6 - \log_2 \log_2 y} & = 1 \end{aligned}$

Let $f(y) = \frac{8}{y} + \frac{2 - \log_2 3}{\log_2 6 - \log_2 y} + \frac{1}{\log_2 6 - \log_2 \log_2 y}$ We can perform a few tests on $f$ to get a feeling of its behavior.

Especially, plugging in powers of 2 allows us to simplify the function expression. Using that approach, we find that $f(8) = 1$ . This means $\log_2 x = 8$ , and so it follows that $\boxed{x = 256}$

I would be curious to see a pure algebraic solution :-).

simply substituting x = 256 1 +.75 - .75 = 1