Lots of ratio

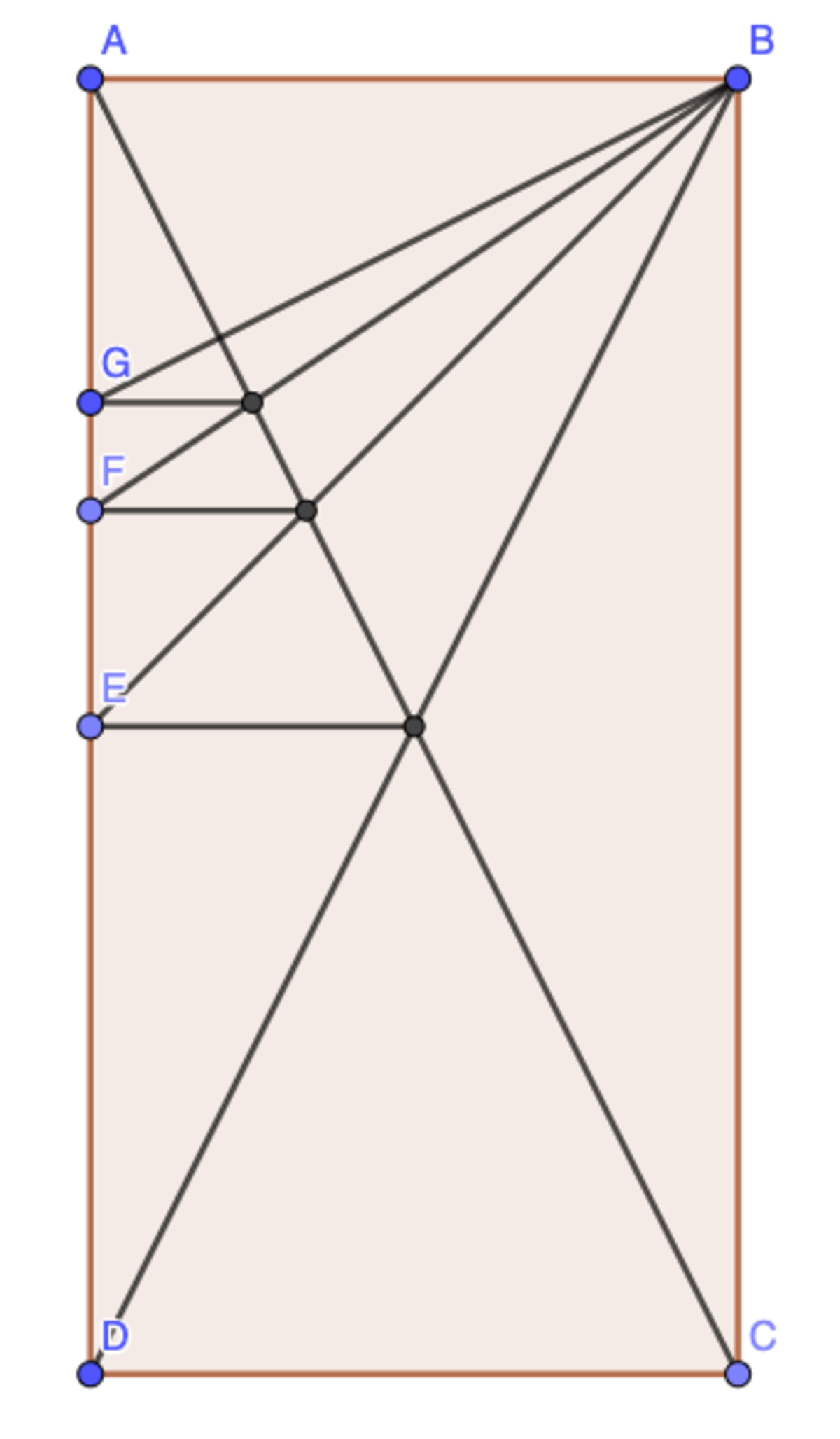 A
B
C
D
is a rectangle and the lines ending at
E
,
F
and
G
are all parallel to
A
B
, as shown. If
A
D
=
1
2
, what is
A
G
?
A
B
C
D
is a rectangle and the lines ending at
E
,
F
and
G
are all parallel to
A
B
, as shown. If
A
D
=
1
2
, what is
A
G
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
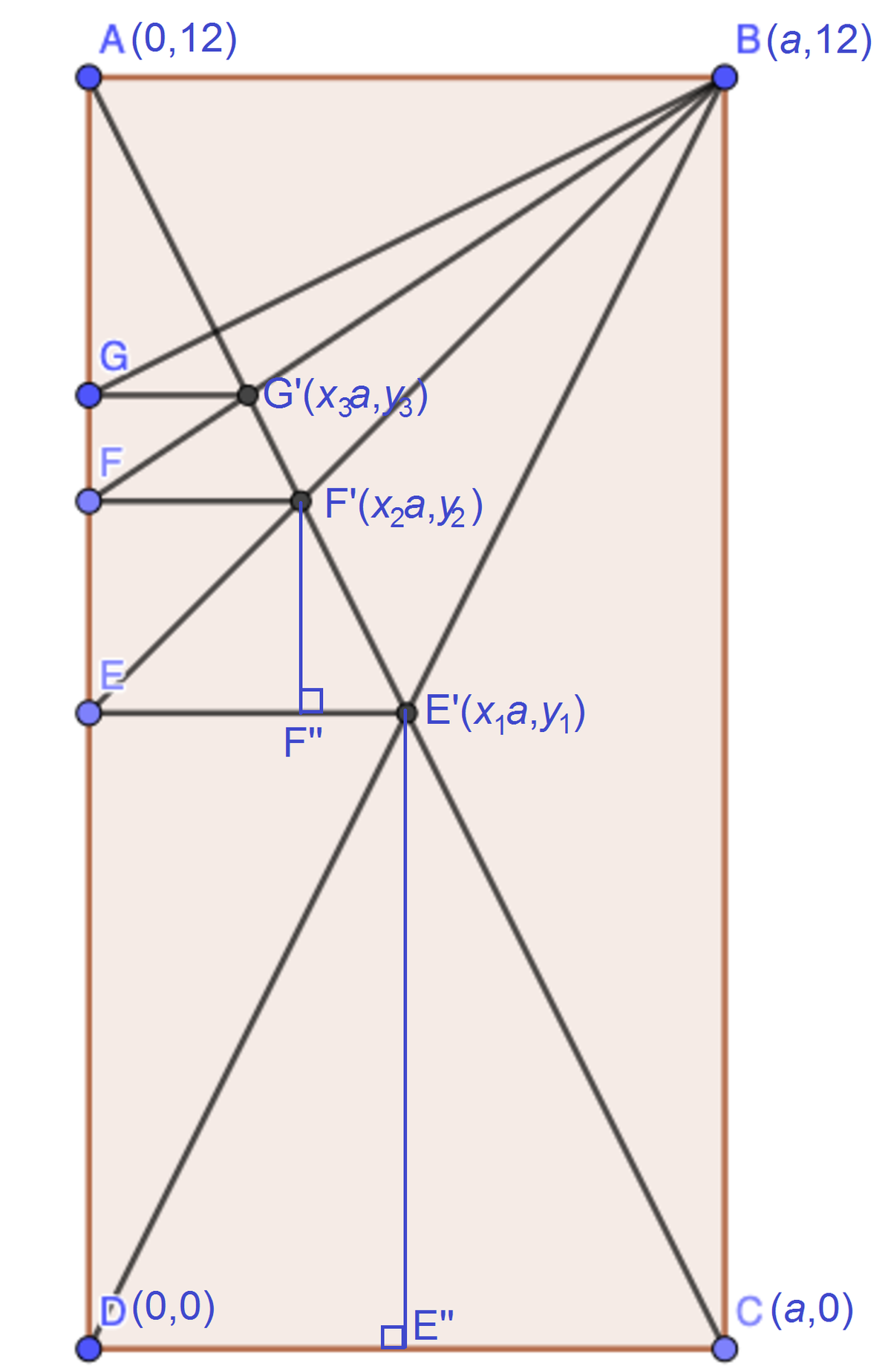
Let D be the origin ( 0 , 0 ) of an x y -plane. The length of A B = C D = a . Let the other ends of the three short parallel lines be E ′ ( x 1 a , y 1 ) , F ′ ( x 2 a , y 2 ) , and G ′ ( x 3 a , y 3 ) . Let us find the recursive relation of { x n , y n } . First consider a general case of ( x 2 , y 2 ) .
Let E ′ E ′ ′ and F ′ F ′ ′ be perpendicular to C D and E E ′ respectively. Due to similar triangles we have:
⎩ ⎪ ⎨ ⎪ ⎧ F ′ F ′ ′ E F ′ ′ = B B ′ E B ′ F ′ F ′ ′ F ′ ′ E ′ = A B C D ⟹ y 2 − y 1 x 2 = 1 2 − y 1 1 ⟹ y 2 − y 1 x 1 − x 2 = 1 2 1 . . . ( 1 ) . . . ( 2 )
( 2 ) ( 1 ) : x 1 − x 2 x 2 = 1 2 − y 1 1 2 ⟹ x 2 = 2 4 − y 1 1 2 x 1 ⟹ x n = 2 4 − y n − 1 1 2 x n − 1
( 2 ) : ⟹ y 2 = 1 2 ( x 1 − x 2 ) + y 1 ⟹ y n = 1 2 ( x n − 1 − x n ) + y n − 1
We can easily find that x 1 = 2 1 and y 1 = 6 , then
x 2 = 2 4 − 6 1 2 × 2 1 = 3 1 x 3 = 2 4 − 8 1 2 × 3 1 = 4 1 ⟹ y 2 = 1 2 ( 2 1 − 3 1 ) + 6 = 8 ⟹ y 3 = 1 2 ( 3 1 − 4 1 ) + 8 = 9
We note that A G = A D − G D = 1 2 − y 3 = 3 .
Let the position coordinates of A , B , C , D be ( 0 , 1 2 ) , ( a , 1 2 ) , ( a , 0 ) , ( 0 , 0 ) respectively. Then those of E are ( 0 , 6 ) and the equation of A C is
y = − a 1 2 x + 1 2 .
Equation of B E is
y = a 6 x + 6 .
Solving, the y -coordinate of F is 8 , and the equation of B F is
y = a 4 x + 8 .
So, the y -coordinate of G is 9 and ∣ A G ∣ = 1 2 − 9 = 3 .
Then U T P U = a r ( △ Q U T ) a r ( △ P U Q )
And U T P U = a r ( △ S U T ) a r ( △ P U S )
Using the above two equation we get
U T P U = a r ( △ S Q T ) a r ( △ P Q S ) = n + 1 1 a r ( △ S Q R ) 2 1 a r ( P Q R S ) = n + 1 1 2 1 a r ( P Q R S ) 2 1 a r ( P Q R S ) = n + 1
With reference to the diagram of Chew-Seong Cheong's solution
Let A B = a and it is given A D = 1 2 . Then clearly E E ′ = 2 a and A E = 6
Now applying the concept shown above we will get
F ′ E ′ A F ′ = 1 + 1 = 2
So, F E A F = F ′ E ′ A F ′ = 2
⇒ A F = 4
Applying that concept again
G ′ F ′ A G ′ = 2 + 1 = 3
So, G F A G = G ′ F ′ A G ′ = 3
⇒ A G = 3