Lots of Squares or One Big One?

Algebra Level 2

There is a square in Shape A, and infinite squares in Shape B. Each additional square from left to right forms a converging geometric progression of areas.

If the area of Area of Blue Shape = Area of Yellow Shape \color{#3D99F6}{\text{Area of Blue Shape}} = \color{#CEBB00}{\text{Area of Yellow Shape}} , what is the value of x x to three decimal places?

Inspiration


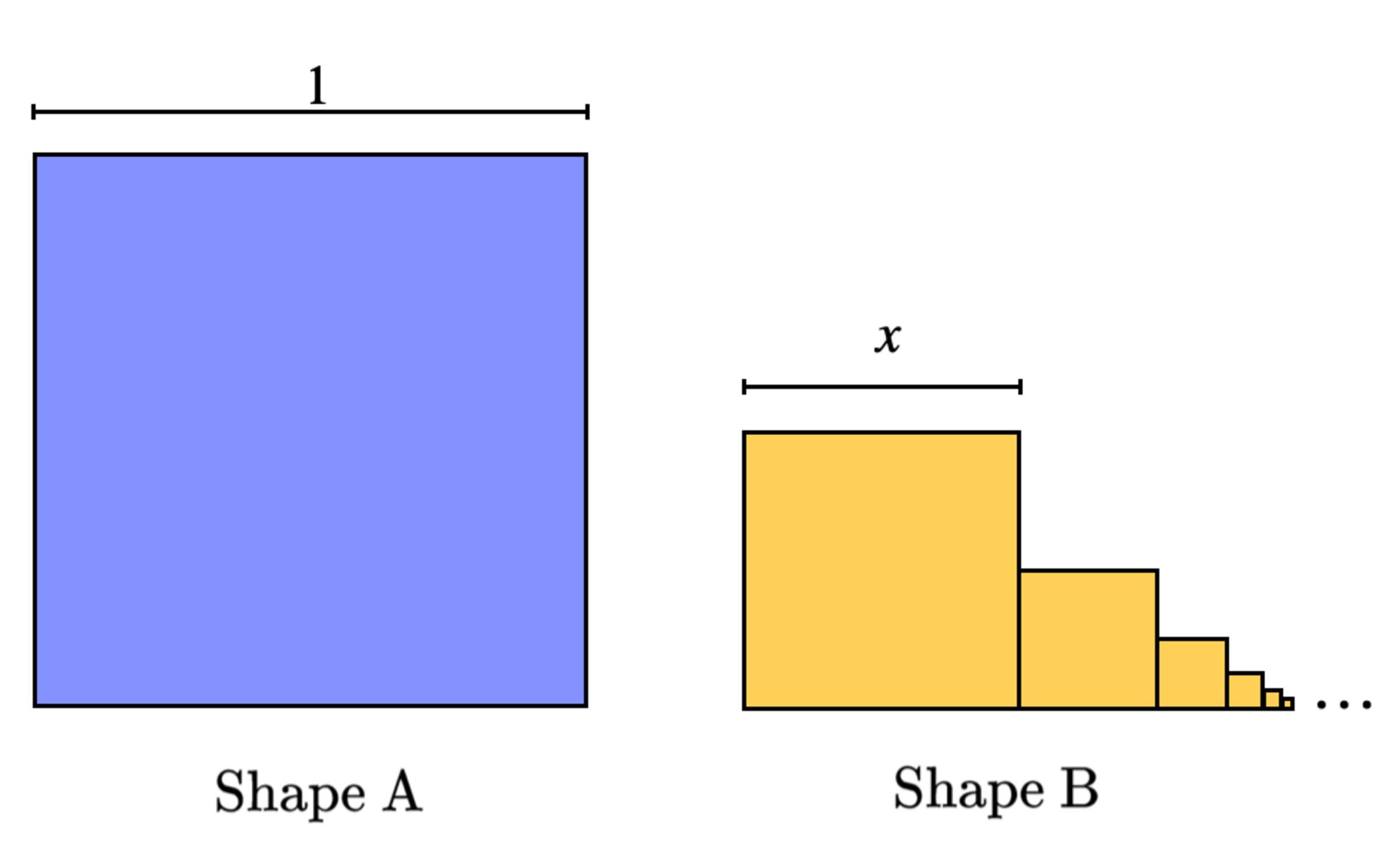
The answer is 0.707.

Mahdi Raza by Mahdi Raza , 16, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Mahdi Raza
Apr 10, 2020

Area of Blue Shape = Area of Yellow Shape 1 = x 2 + x 4 + x 6 + x 8 … 1 = x 2 1 − x 2 Sum of converging G.P. 1 − x 2 = x 2 1 = 2 x 2 x 2 = 1 2 x = + 1 2 , − 1 2 x = + 1 2 [ ∵ x ≠ − v e ] \begin{aligned} \color{#3D99F6}{\text{Area of Blue Shape}} &= \color{#CEBB00}{\text{Area of Yellow Shape}} \\ \color{#3D99F6}{1} &= \color{#CEBB00}{x^2 + x^4 + x^6 + x^8 \ldots} \\ \color{#3D99F6}{1} &= \color{#CEBB00}{\frac{x^2}{1 - x^2}} \quad \color{#333333}{\text{Sum of converging G.P.}} \\ \\ 1-x^2 &= x^2 \\ 1 &= 2x^2 \\ x^2 &= \frac{1}{2} \\ x &= + \frac{1}{\sqrt{2}}, - \frac{1}{\sqrt{2}} \\ x &= + \frac{1}{\sqrt{2}} \quad [\because x \ne -ve] \end{aligned}

x ≈ 0.707 \boxed{x \approx 0.707}

4 Helpful 0 Interesting 0 Brilliant 0 Confused

This question, as stated, may not be well-defined. For example, the sequence x^2, (rx)^2, (r^2x)^2, (r^3 x)^2, ... is also a convergent geometric progression of areas. But the total area would then depend on r, the only requirement being that 0 < r < 1. For a specific example, if the side length of each square decreases by half (r = 1/2), then the answer to this problem would be x = 0.866.

Doug Brunson - 1 year, 2 months ago

Log in to reply

I don't clearly understand what you are trying to say.. Though from whatever I understood, it is given that area of Blue and Yellow is equal. Thus only one type of G.P. should exactly equal the area fo blue which is 1... and that series is 1/2 + 1/4 + 1/8 + 1/16. In this case x^2 = 1/2. Which means x = 1 / 2 1/\sqrt{2} = 0.707

Mahdi Raza - 1 year, 2 months ago

I was just trying to argue that your problem has one free variable: the geometric ratio, r. In your solution, you are saying that the geometric ratio (side length ratio) is r = x. This makes for an interesting solution, but it is not the only solution.

Doug Brunson - 1 year, 2 months ago

Oh... I see. You are saying that the ratio is x (moving from blue to yellow square on the right). Sorry, I didn't catch that.

Doug Brunson - 1 year, 2 months ago
David Vreken
Apr 10, 2020

Using the following pattern of triangles, Shape A can be divided in half, then the remaining area can be divided in half again, and that remaining area can be divided in half again, and so on, and those triangles can be rearranged to make the different squares in Shape B:

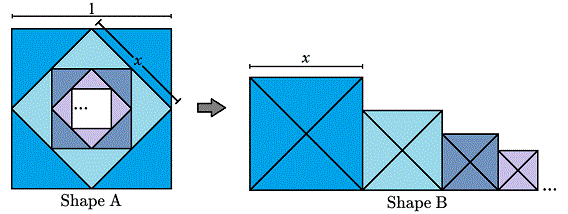
Each square follows a geometric progression by a ratio of 1 2 \frac{1}{2} , and x x solves to x = 2 2 ≈ 0.707 x = \frac{\sqrt{2}}{2} \approx \boxed{0.707} .

0 Helpful 0 Interesting 2 Brilliant 0 Confused

@David Vreken Great solution and Thanks!!

Mahdi Raza - 1 year, 2 months ago

Thanks for this solution! I wouldn't have understood this question without your help...

A Former Brilliant Member - 1 year ago

2 pending reports

Vote up reports you agree with

×

Problem Loading...

Note Loading...

Set Loading...