Lots of Squares
 Compute the value of:
Compute the value of:
1 2 − 3 2 + 5 2 − 7 2 . . . + 9 7 2 − 9 9 2 .
The answer is -5000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Nice one. You're welcome for the problem haha.
Obviously it's sum and difference of squares. Try to factor out.. ( 1 2 − 3 2 ) + ( 5 2 − 7 2 ) + ( 9 2 − 1 1 2 ) . . . + ( 9 7 2 − 9 9 2 )
( 1 − 3 ) ( 1 + 3 ) + ( 5 − 7 ) ( 5 + 7 ) + ( 9 − 1 1 ) ( 9 + 1 1 ) . . . + ( 9 7 − 9 9 ) ( 9 7 + 9 9 )
( − 2 ) × [ 4 + 1 2 + 2 0 . . . + 1 9 6 ]
( − 8 ) × [ 1 + 3 + 5 . . . + 4 9 ]
For the odd series..
a n = 2 n + 1
4 9 = 2 n + 1
n = 2 5 ---> the nth term of the series
For the sum of odd series
S n = [ 2 n ] ( 2 a 1 + ( n − 1 ) d )
S n = [ 2 2 5 ] ( ( 2 ) ( 1 ) + ( 2 5 − 1 ) ( 2 ) )
S n = 6 2 5
therefore:
− 8 × 6 2 5 = − 5 0 0 0
I also used AP, but i took into consideration of 97 as 49th odd number and n as 49, why did u take n as 25??????????
S of n = n/2( 2a + (n-1)d) , { S of n means sum of AP},
n=49 as ( 97 is the 49th odd number) , a =-8, d=-16,
S of 49 = 49/2( -16 + 48*-16),
S of 49 = 49/2 * -784,
S of 49 = -19208, i am not getting 5000, where am i going wrong???
Log in to reply
hmm.. from the very start, ur doing it wrong.. why is ur n equals to 4 9 ?
if I am going to use ur values of a 1 and d that u use, then ur series must be like these..
− 8 + − 2 4 + − 4 0 + − 5 6 + − 7 2 . . . + − 3 7 6 + − 3 9 2
in that case , the value of a 1 is − 8
then for the value of d , it is − 1 6 , just like what u use from the start..
then this will be ur formula for that series..
a n = − 8 ( 2 n + 1 )
in ur case, why will u take the consideration that n = 4 9 . when 9 7 doesn't exist from the series that u create?
actually, ur doing it right from the start, but u messed up from the part of taking value of n , which is the most important thing from these process. these part is the correction of what u are doing.. remember, we must not assume the position of a certain of number from a series without knowing the formula for the series. by using the formula of the series above, we can get the value of n wherein the value of a n is the last number of the series, which is − 3 9 2 .
− 3 9 2 = − 8 ( 2 n + 1 )
n = 2 5
For the sum of odd series
S n = [ 2 n ] ( 2 a 1 + ( n − 1 ) d )
S n = [ 2 2 5 ] ( ( 2 ) ( − 8 ) + ( 2 5 − 1 ) ( − 1 6 ) )
S n = − 5 0 0 0
i made pairs of 99-1 , 97-3..............so on.........and calculated using A.P summation
1^2-3^2+5^2-7^2+...+97^2-99^2
= (1-3)(1+3)+(5-7)(5+7)+...+(97-99)(97+99)
= -2(4+12+...+196)
= -2(4+196)[(196-4)/8+1]
= -5000
The answer is simply {The negative difference of the [(negative of 49th summation of (unbounded) 9409 (where n is equivalent to 1) and 9784] = (-5000)} where it can be clearly stated as -5000 which is the correct answer !
1^2-3^2 + 5^2-7^2 ... + 97^2-99^2 (1+3)(1-3) + (5+7)(5-7) ... + (97+99)(97-99) (4)(-2) + (12)(-2) ... + (196)(-2) -2[(4) + (12) ... + (196)] The sum of 4,12 ..., 196 (25 terms) S = n/2 (1st term + Last term) where n = number of terms S = 25/2 (4+196) S = 25/2 (200) S = 25 (100) S = 2500
-2(2500) -5000
1^2 - 3^2 = -2(4)
5^2 - 7^2 = -2(12)
9^2 - 11^2 = -2(20)
...............................
97^2 - 99^2 = -2(196)
Adding
The given number = -2(4 + 12 + 20 + ........... + 196) = -2(sum of arithmetic sequence)
Then
The given number = -2(2500) = - 5000
Group in parentheses: ( 1 2 − 3 2 ) + ( 5 2 − 7 2 ) + . . . ( 9 7 2 − 9 9 2 )
Each parenthesis is a difference of two squares, so you can rewrite it as: ( 1 − 3 ) ( 1 + 3 ) + ( 5 − 7 ) ( 5 + 7 ) + . . . ( 9 7 − 9 9 ) ( 9 7 + 9 9 )
Notice that for each product, the factor that involves a subtraction always equals -2 (1-3=-2, 5-7=-2, 97-99=-2), so you can rewrite it as: − 2 ( 1 + 3 ) + − 2 ( 5 + 7 ) + . . . − 2 ( 9 7 + 9 9 )
You can factor out a -2: − 2 ( 1 + 3 + 5 + 7 + . . . 9 7 + 9 9 )
The term in parenthesis is a simple arithmetic series where a 1 = 1 , n = 5 0 , a 5 0 = 9 9 So that whole series equals 2 5 0 ( 1 + 9 9 ) = 2 5 0 ( 1 0 0 ) = 2 5 0 0 0 = 2 5 0 0 Replace (1+3+5+7+... 97+99) with 2500 and:
− 2 ( 2 5 0 0 ) = − 5 0 0 0
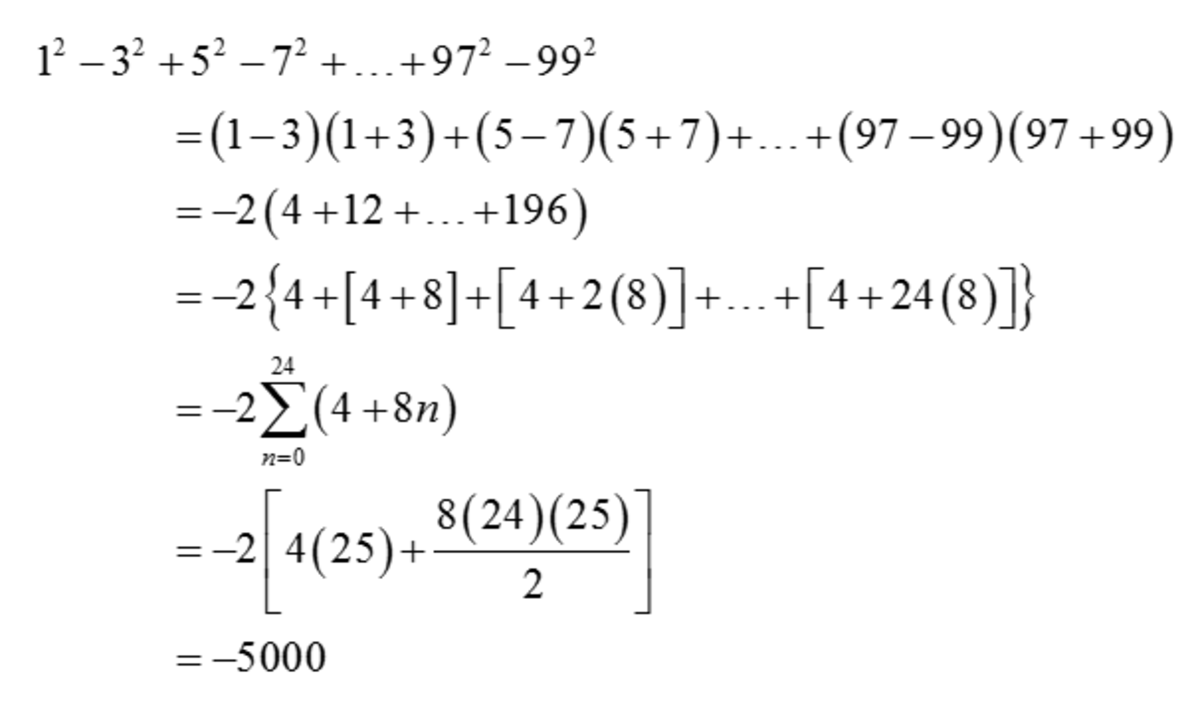
Group with parentheses:
( 1 2 − 3 2 ) + ( 5 2 − 7 2 ) . . . + ( 9 7 2 − 9 9 2 )
Evaluate each group of parentheses:
( − 8 ) + ( − 2 4 ) + ( − 4 0 ) . . . + ( − 3 9 2 )
Factor out − 8 . We know each term must be a multiple of − 8 because x 2 − ( x + 2 ) 2 = − 4 ( x + 1 ) , and since x is always odd, x + 1 is always even, so − 4 ( x + 1 ) must always be a multiple of − 8 .
− 8 ( 1 + 3 + 5 . . . + 4 9 )
The sum of the odd numbers from 1 to 49 is 2 5 0 ∗ 2 5 or 6 2 5 .
− 8 ∗ 6 2 5 = − 5 0 0 0