Love Circles
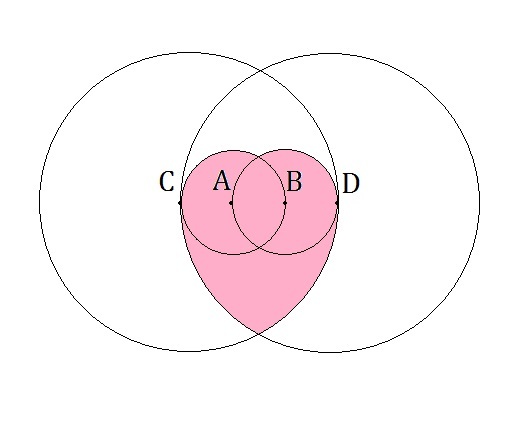
The points A , B , C , D are the centers of the circles as shown above. The circles A and B each have a radius of length 1 cm. and pass through each other's center. Similarly, the circles C and D each have a radius of length 3 cm. and also pass through each other's center, inscribing the smaller circles inside the overlapping portion.
What is the area of the pink section (in cm 2 )? Give your answer in the nearest 3 decimal places.
The answer is 8.055.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Did the same thing but made a calculation mistake. The answer I input was 8.175 and I got it write. How come?
lol, I got the same final answer, but my calculator just outputted 3 different wrong answers :P
How triangle ABE is equilateral
Got the same solution! :)
The pink area={(1/2)the big common area}+{ 2 * Small half circles}-{(1/2)the small common area}
Pink area=big segment area with 120 degrees + full small circle - small segment area with 120 degrees
=
{
3
π
∗
3
2
−
2
∗
2
1
∗
2
3
∗
3
∗
2
3
}
+
π
−
(
3
π
−
4
3
)
.
=
{
3
π
−
4
9
∗
3
}
+
π
−
3
π
+
4
3
=
3
3
2
π
−
2
3
=
8
.
0
5
5
1
What is the area X of the intersection between two circles of radius r each passing through the other's centre? This area can be divided into two congruent equilateral triangles with side r and 4 equivalent curvilinear portions. The area say A of the equilateral triangle is: A = 4 r 2 3 . The area say S of the curvilinear portion is the area of the circular sector, with angle π / 3 , minus A: S = 6 π r 2 − A . Therefore, X = 4 S + 2 A = 3 2 π r 2 − 2 3 r 2 . If you like calculus, you can determine this value also by integration: X = 4 ∫ r / 2 r d x r 2 − x 2 = 4 [ 2 x r 2 − x 2 + 2 r 2 arcsin r x ] r / 2 r = 3 2 π r 2 − 2 3 r 2 . Now, what is the area Y of the figure made by the two intersected circles? It is the area of the two circles minus the area of the intersection (because otherwise it would be taken into account twice): Y = 2 π r 2 − X = 3 4 π r 2 + 2 3 r 2 . Finally, we can conclude that the area P of the pink, heart-shaped :), region under investigation is: P = 2 X ( r = 3 ) + 2 Y ( r = 1 ) = 3 1 1 π − 2 3 . Rounding up the numerical value: P ≈ 8 . 0 5 5 .
Let point E be the upper intersection point of the circles A & B and point F be the lower intersection point of the circles C & D.
By drawing a line CD, passing through all centers, we can split the shaded area into 2 parts: the area above and below the line CD.
The pink area above the line CD = (portion CAE) + (portion DBE) + (equilateral triangle ABE)
The circular portions CAE and DBE both have 120 degrees out of 360 portion (since the equilateral triangle has equal angles of 60 degrees, 180 - 60 = 120 degrees).
Therefore, both portions add up to 2( 3 π )( 1 2 ) = 3 2 π .
Hence, the area above the line CD = 3 2 π + 4 3 ( 1 2 ) = 3 2 π + 4 3 .
Now the pink area below the line CD = (portion CDF) + (portion DCF) - (equilateral triangle CDF)
Even though the portions CDF & DCF have different centers and arcs, they both have the 3 6 0 6 0 = 6 1 portion of the big circle. Hence, the area of both portions = 2( 6 π )( 3 2 ) = 3 π .
However, by adding these portions together, we have an excess of the overlapping equilateral triangle, so we have to subtract this area out.
Therefore, the pink area below the line CD = 3 π - 4 3 ( 3 2 ) = 3 π - 4 9 3 .
Finally, the total pink area = 3 2 π + 4 3 + 3 π - 4 9 3 = 3 1 1 π - 2 3 ≈ 8.055 c m . 2