A Triangle Evolves Into A Hexagon
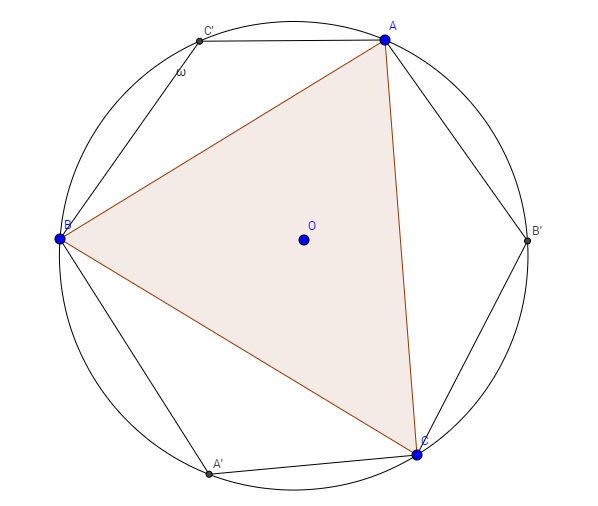
Consider an acute angled Δ A B C with circumcircle ω and circumcenter O . Now, construct points (on the circumcircle) diametrically opposite to the vertices of the triangle, and name them A ′ , B ′ and C ′ as shown in the figure. The area of Δ A B C is 1 8 square units.
Find the area of polygon A B ′ C A ′ B C ′ .
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Well, there is a simple synthetic approach. Do try to think about it !
Hint : It is sufficient if you know that median divides a triangle into those of equal area to solve this problem.
Log in to reply
Nice. Since O is the midpoint of A A ′ and B B ′ , we have ∣ A O B ∣ = ∣ A O B ′ ∣ = ∣ A ′ O B ∣ , and similarly for the other two triangles A O C and B O C . Thus ∣ A B ′ C A ′ B C ′ ∣ = = ∣ A O B ′ ∣ + ∣ B ′ O C ∣ + ∣ C O A ′ ∣ + ∣ A ′ O B ∣ + ∣ B O C ′ ∣ + ∣ C ′ O A ∣ 2 ( ∣ A O B ∣ + ∣ A O C ∣ + ∣ B O C ∣ ) = 2 ∣ A B C ∣
nice! I think taking the limiting situation i.e cconsidering the triangle to be equilateral and hence the formed hexagon as regular will do.
Log in to reply
If you take the approach that the answer to the question must be independent of the shape of the triangle (since otherwise they would not ask the question in the first place), then going with an equilateral triangle will, of course, get you the answer quickly.
It won't tell you why the result holds for all other triangles, though...
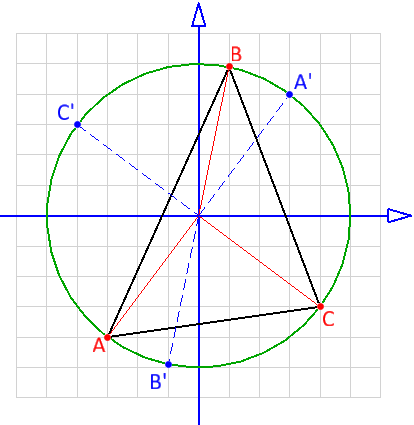
Let A ( x 1 , y 1 ) , B ( x 2 , y 2 ) , C ( x 3 , y 3 ) be the three vertices.
Points diametrically opposite to these would be their reflections about the origin: A ′ ( − x 1 , − y 1 ) , B ′ ( − x 2 , − y 2 ) , C ′ ( − x 3 , − y 3 )
Area of Δ A B C = 2 1 ∣ ∣ ∣ ∣ ∣ ∣ x 1 x 2 x 3 y 1 y 2 y 3 1 1 1 ∣ ∣ ∣ ∣ ∣ ∣ this expands into six terms.
Area expressions of the three peripheral triangles A'BC, AB'C, ABC' will be identical except for the sign of four terms (which would cyclically vary for the three triangles).
In the sum of the peripheral areas, each term would appear thrice - once with one sign and twice with opposite signs. The pair with opposite sign would cancel out, leaving behind just one instance of each term in the sum. Which will be nothing but the expression for the area of Δ A B C
Method II (This is probably not what Karthik has in mind, but found the cyclic nature of these areas interesting)
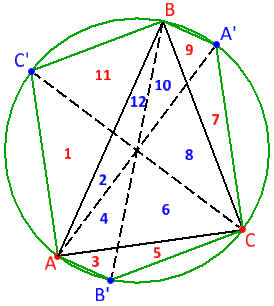
The areas can be numbered as shown (have used even for original triangle, odd for the peripherals) If the diameters AA', BB', CC' are taken as bases, then the other radii become the medians. Then the areas 1, 3, 5, 7, 9, 11 can be expressed as
1 = 4 + 6 - 2
3 = 2 + 12 - 4
5 = 8 + 10 - 6
7 = 4 + 6 - 8
9 = 2 + 12 - 10
11 = 8 + 10 - 12
(1+3+5+7+9+11) = (2+4+6+8+10+12) as required
Co-ordinate bash seems fine, but there is a simple one-liner solution if you solve it synthetically. See Mark Henning's comment.
Log in to reply
Thanks for letting me know, I will look for another approach.
Woahhh! I didn't know bashing is a possible solution as well!!! Thank you!
Nice approach :) !
Is it right to consider it an equilateral triangle and then solve?
To be precise, no, because the problem statement did not mention so. But if you just need the answer , you can consider the equilateral triangle case and compute easily.
OAC' +OBC'+OA'B+OA'C+OB'C+OAB' is area of hexagon. This is OAC+OBC+OAB+OAC+OBC+OAB. Hence twice area of triangle
Trick solution: Consider △ A B C as a equilateral triangle. It becomes immediately obvious that A B ′ C A ′ B C ′ is a regular hexagon. Since △ A O B ≅ △ A C ′ B , △ B O C ≅ △ B A ′ C and △ C O A ≅ △ C B ′ A , we can deem that the area of the polygon is twice the area of the equilateral triangle and hence the area is 36.
(This isn't a proof, it's just how I got the right answer.
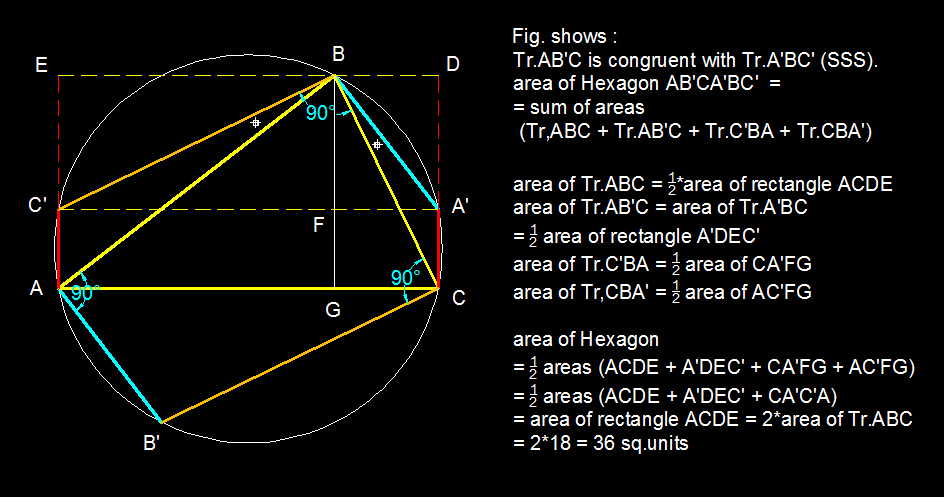
Let R be the radius of the circumcircle. The quadrilateral B C B ′ C ′ is a rectangle, and B C ′ = 4 R 2 − a 2 = a 2 c o s e c 2 A − a 2 = a cot A using the extended Sine Rule, and so B C B ′ C ′ has area a 2 cot A . Similarly the rectangle A C A ′ C ′ has area b 2 cot B , while the rectangle A B A ′ B ′ has area c 2 cot C . The sum of these three rectangle areas, namely a 2 cot A + b 2 cot B + c 2 cot C is equal to the area of the hexagon plus twice the area of the triangle A B C .
On the other hand, the triangle O B C has area 2 1 R 2 sin 2 A = 8 1 a 2 c o s e c 2 A sin 2 A = 4 1 a 2 cot A , and hence the area of the triangle A B C can be written as 4 1 ( a 2 cot A + b 2 cot B + c 2 cot C ) . Thus four times the area of the triangle is the area of the hexagon plus twice the area of the triangle. Thus the area of the hexagon is twice the area of the triangle, namely 3 6 square units.