Love for geometry-4
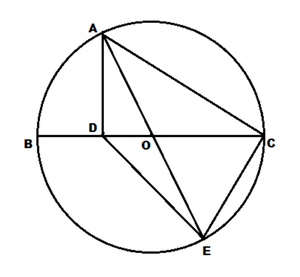
Let be a diameter of a circle having center and be a point on such that . Let and be points on the circle such that is perpendicular to and passes through . If , then , find .
Note: denotes the area.
The answer is 12.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the radius of the circle be r . Then A O = E O = r . Since B D = 3 D C and B C = 2 r , ⟹ B D = 2 r , D C = 2 3 r , and D O = 2 r . This means that △ A B D and △ A D O are similar. Therefore A O = A B ⟹ r = 4 . We note that △ A D C and △ C D E share a common base of D C and have heights A D and E F respectively. Since △ A D O and △ O E F are similar, A D = E F . Therefore △ A D C and △ C D E have the same area. Then
[ A D E C ] ⟹ 3 [ A D E C ] = [ A D C ] + [ C D E ] = 2 [ A D C ] = 2 × 2 1 × A D × D C = 2 × 2 1 × 2 3 × 6 = 1 2 3 = 1 2