Love of food

There are three families in a certain restaurant. The first family bought 2 Spaghetti's, 4 French fries and 6 glasses of Juice and it cost them 110 coins.
The second family bought 3 Spaghetti's, 8 French fries and 3 glasses of Juice and it cost them 155 coins.
The third family bought 5 Spaghetti's, 2 French fries and 10 glasses of Juice and it cost them 170 coins.
My question is, if I will buy a spaghetti, a french fry and a glass of juice, how much would it cost me?
The answer is 35.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
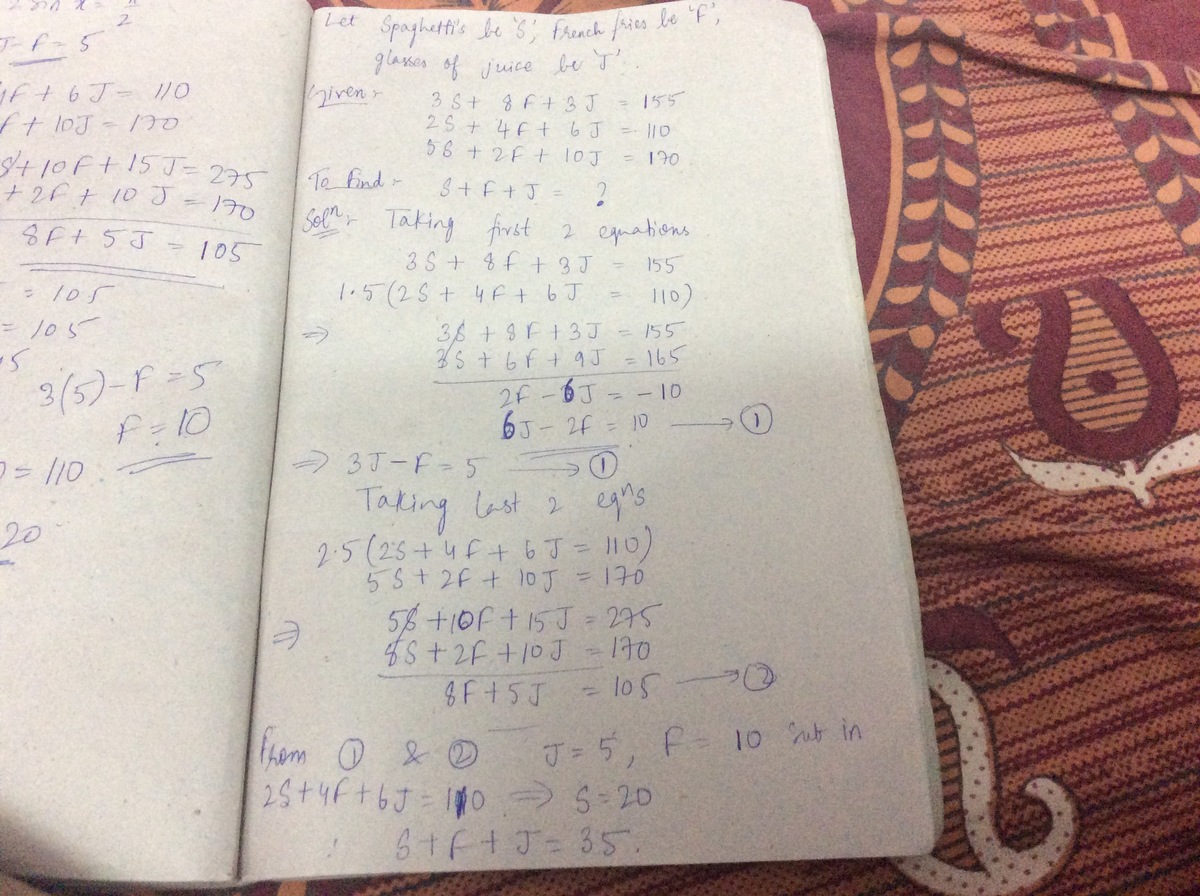
WE WILL SOLVE IT USING SYSTEMS OF LINEAR EQUATIONS, WE WILL LET THE PRICE OF THE SPAGHETTI AS X,THE FRIES AS Y AND THE JUICE AS Z. SO WE HAVE THE EQUATIONS:
2X+4Y+6Z=110 3X+8Y+3Z=155 AND 5X+2Y+10Z=170
AND BY SOLVING...
2(2X+4Y+6Z=110)-->4X+8Y+12Z=220 AND BY PAIRING IT WITH 3X+8Y+3Z=155 WE CAN USE ELIMINATION TO ELIMINATE 8Y SO WE HAVE X+9Z=65
AND ANOTHER IS 2(5X+2Y+10Z=170)-->10X+4Y+20Z=340 AND BY PAIRING IT WITH 2X+4Y+6Z=110 WE CAN USE ELIMINATION TO ELIMINATE 4Y SO WE HAVE 8X+14Z=230 AND BY PAIRING IT WITH X+9Z=65 WE GOT X=65-9Z AND SUSTITUTE IT TO 8X+14Z=230 8(65-9Z)+14Z=230 520-72Z+14Z=230 -58Z=-290 Z=5 WHICH IS THE PRICE FOR OUR JUICE
AND WE WILL SUSTITUTE THIS VALUE TO GET THE VALUE OF OUR X X+9Z=65 X+9(5)=65 X+45=65 X=65-45 X=20 WHICH IS THE PRICE FOR OUR SPAGHETTI
AND LASTLY,WE WILL GET THE PRICE OF OUR FRENCH FRIES 2X+4Y+6Z=110 2(20)+4Y+6(5)=110 40+4Y+30=110 4Y+70=110 4Y=110-70 4Y=40 Y=10
SO IF I WILL BUY A SPAGHETTI,A FRENCH FRY AND A GLASS OF JUICE, IT WOULD COST ME 20+10+5 =35 COINS ALL IN ALL