Lovely Heart Curve!
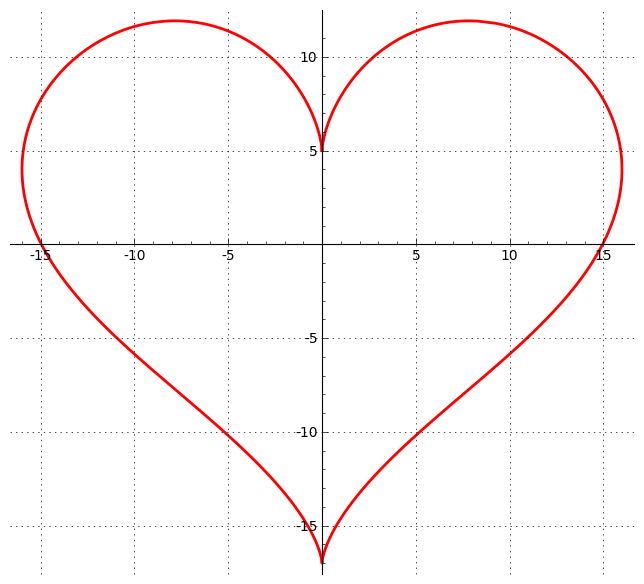 Image Credit: Penguin
Image Credit: Penguin
Mai Valentine and Joey Wheeler continued to decide what to decorate for the party. Instead of copying the graph above formed by the following parametric equations x ( t ) y ( t ) = 1 6 sin 3 ( t ) = 1 3 cos ( t ) − 5 cos ( 2 t ) − 2 cos ( 3 t ) − cos ( 4 t )
they thought that creating the wave related to the heart curve, similar to the following example:
 Image Credit: Wikipedia
Image Credit: Wikipedia
However, since some of their friends dislike jump discontinuities , they were concerned that
For all real t , the wave graph of the parametric equations contains at least a jump discontinuity.
Does there exist a jump discontinuity of the wave graph, or were Joey and Mai imagining?
This is the end of third chapter of the story . Check out the following chapters:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
This is excellent. What tools did you use to create this visual?
In fact, this curve, if expressed in true polar form r ( θ ) , would be like more like this

This is what one would see if the polar angle varied at a constant rate instead of at a parametric rate. It's doubtful if there's a closed form expression for this polar curve.
Here, the lowest point of curve is at the cusp at the top of the heart.
Log in to reply
I don't think there is a neatest way to determine the polar equation of the given parametric equations. Solving for t for x ( t ) is a monstrosity, which gives y ( x ) with tons of messy expressions.
Regardless of the differentiability, x ( t ) and y ( t ) are both continuous. Because the parametric curve depends on both x ( t ) and y ( t ) , there wouldn't be another strong reason to back this up. My solution isn't "proof-without-words", but it's visually obvious that based on the graphs of x ( t ) and y ( t ) , the problem is trivial.
Log in to reply
That's right, the polar function that I've come up is actually only a numerical approximation. As I already said, I doubt if there's a closed form expression for it. But now, given the parametric equations you've posted, even though the "lovely heart curve!" looks nice and at least not discontinuous, how do we know that other than by plotting it? I am arguing that because your parametric equations are 1) continuously differentiable, and 2) periodic, there are no jump discontinuities. I am just trying to answer Pi Han Goh's question, which isn't trivial, even though you are saying it is trivial. What is a sufficient (but not necessarily necessary) condition for not having any jump discontinuities?
There is no jump discontinuity of the wave graph. Here are the graphs of x ( t ) and y ( t ) on the usual Cartesian plane:
Is there a systematic way to figure this out without resorting to plotting the graphs?
Log in to reply
Given a "lovely heart curve!", there could be more than one way to express it as a function, so we are really asking ourselves if there are any discontinuities with this one particular parametric form. First of all, we can rule out any point discontinuities since both the parametric functions for x and y have no point discontinuities, so that every point on the "lovely heart curve" is being plotted by this set of parametric functions. Next, is there a "jump continuity"? Without proof right now, I believe that if both parametric functions are continuously differentiable (which they are), then there are no jump continuities in the curve plotted, at least over the range where infinities are not involved.
I believe it's quite possible to devise another set of parametric functions plotting this same curve that does have jump discontinuities.
For another way to plot the curve, one can by brute force come up with a polar plot (see graph I've provided in my other comment), which doesn't have any jump continuities. This is to make the point that this question depends on the function used to plot the curve.
There is no jump discontinuity of the wave graph. Here are the graphs of x ( t ) and y ( t ) on the usual Cartesian plane:
As an interesting fun stuff to look at, here is the illustration of the continuous wave graph (related to two equations), which resembles the irregular heart beat: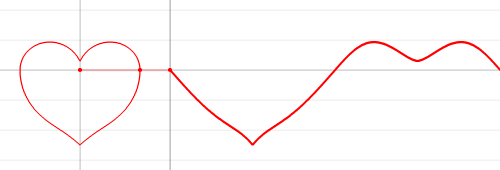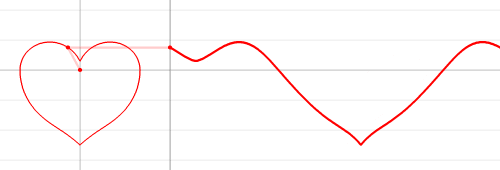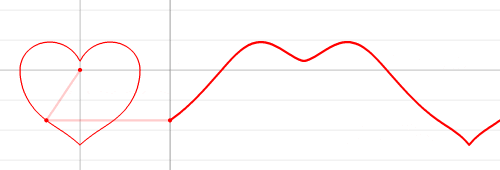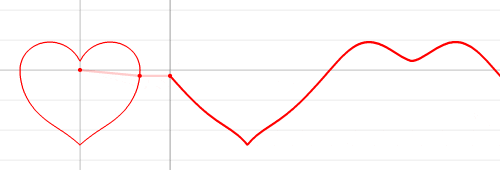 Since both
x
(
t
)
and
y
(
t
)
are continuous, regardless of the cusps, the wave graph is continuous.
Since both
x
(
t
)
and
y
(
t
)
are continuous, regardless of the cusps, the wave graph is continuous.