Lovers Meet - Part 7

Probability Level 2

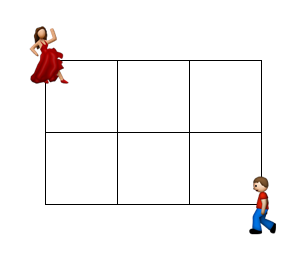Anna and Ben live at opposite corners of a 3 by 4 block.
If Anna only moves right or up or down, and isn't allowed to retrace her steps, how many ways does she have to get to Ben?

16 27 12 24

2 solutions

Daniel Liu
Jul 1, 2015

Consider the last three vertical roads. Anna can choose to enter each vertical road through one of three choices: either the top, middle, or bottom horizontal road.

So the answer is just $3^3=\boxed{27}$ .

I feel like this problems difficulty increased because of the orientation of the grid. the easy solution exists when you consider the problem as her moving left to right, opposed to up and down. if it was oriented as anna could move left and right and only down with the grid flipped into a 3X2 the answer would be more apparent

William Barela - 5 years, 11 months ago

However, the answers would be different in that case.

Chung Kevin - 5 years, 11 months ago

the block arranged 3 long by 2 wide, the only difference would be the orientation. (at least my intent)

William Barela - 5 years, 11 months ago

It's not a 3 by 4 block

Brody Burkett - 3 years ago

Resha Dwika Hefni Al-Fahsi
Jul 4, 2015

I create my own formula:

(i=row; j=coloumn)

If the tiles are 1 x j then,

$\boxed{2^{j}}$

If the tiles are 2 x j then,

$\boxed{3^{j}}$

the conclusion is if the tiles are i x j so

$\boxed{(i+1)^{j}}$

So, $3^{3} = 27$

Can you explain how you arrived at that formula? Is there a simple way of reaching that conclusion?

Chung Kevin - 5 years, 11 months ago

It's incorrect....son numeros combinatorios (5 2)=5!/2!*(5-2)!=10

Humberto Fernández - 4 years, 10 months ago

Lovers Meet - Part 7

2 solutions

0 pending reports