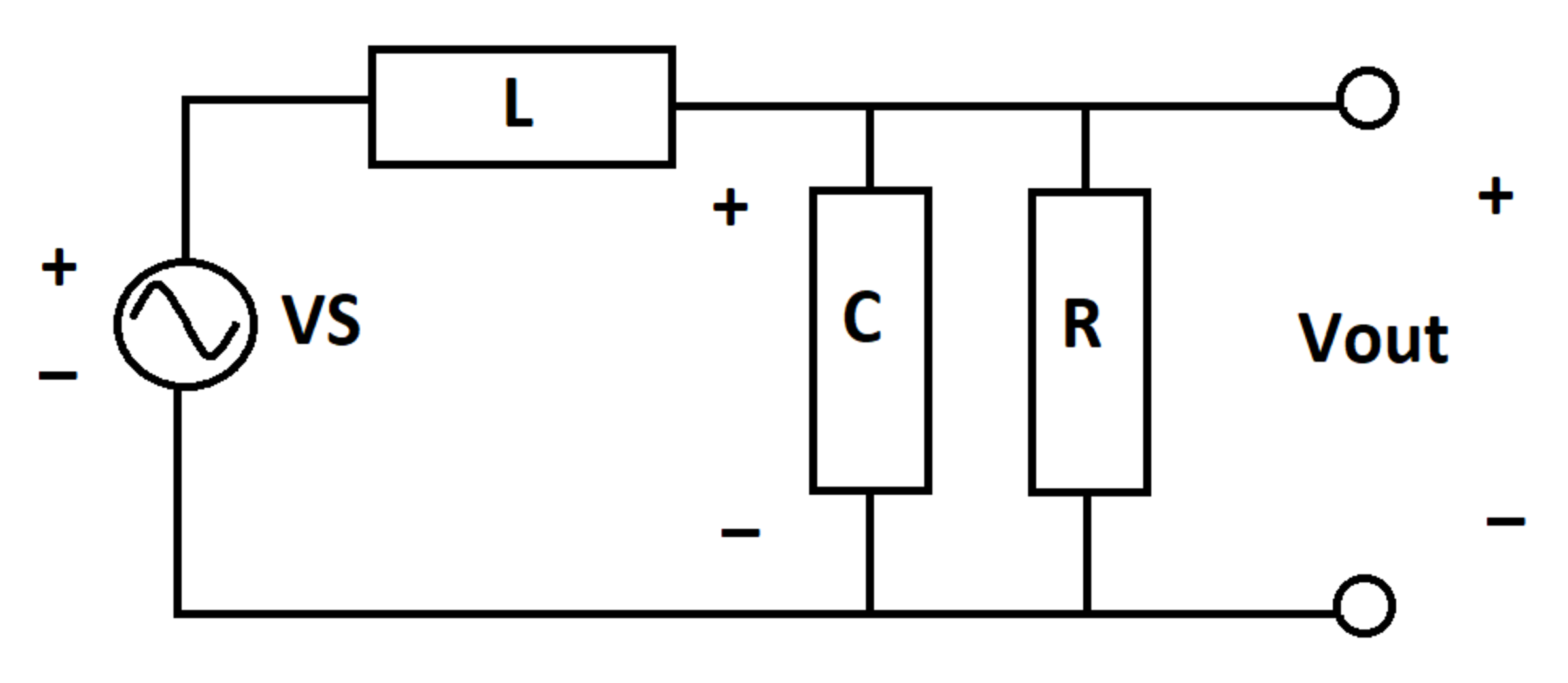
Low Pass Filter Charging Transient

The following solution leaves out several steps and should be thought of as a guideline.

Let the current through the inductor be $I_L$ , that through the capacitor be $I_C$ and that through the resistor be $I_R$ . Let the charge on the capacitor be $Q$ and the output voltage be $V$ . The circuit equations are:

$\blue{I_L = I_C+I_R} \ ; \ \red{L\dot{I}_L + \frac{Q}{C} = V_S} \ ; \ \green{\frac{Q}{C} = I_RR = V} \ ; \ \orange{\dot{Q} = I_C}$

Initial conditions: $Q(0) = 0$ , $I_L(0) = 0$ and using these conditions, those on other variables can be derived. The goal is to come up with a dynamic mapping between $V_S$ and the output $V$ . By manipulating the above equations, the resulting differential equation is:

$\ddot{V} + 2\dot{V} + V = 10\sin{t}$

subject to: $V(0) = 0$ and $\dot{V}(0) = 0$ . This differential equation can be solved using the method of Laplace transforms or any other standard approach. The closed-form solution to this is:

$V = 5 e^{-t}(1+t) - 5\cos{t}$

From here, it can be concluded that the steady state solution is $V_{ss} = -5\cos{t}$ and the required integral to be computed is therefore:

$\boxed{\int_{0}^{10\pi}5 e^{-t}(1+t) dt = 10-5(10\pi+2)e^{-10\pi} \approx 10}$