Lumberjack physics

A perfectly symmetrical tree has a trunk in the shape of a cylinder with diameter 0.2 m. Since the tree is symmetrical the center of mass is at some distance L above the ground along the axis of the cylinder. A rotten lumberjack with no concept that he's cutting down the most amazing tree ever grown uses a chain saw to cut the tree down. He saws horizontally right at the base of the tree (ground level). What is the minimum value of L in meters such that the tree begins to topple over as soon once the chain saw reaches the position in the picture?
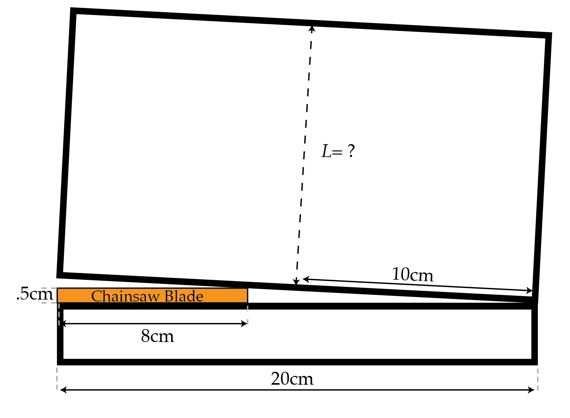
Details and assumptions
- The chain saw blade is 8 cm wide and 0.5 cm high.
- Treat the tree as a rigid body.
The answer is 2.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
We calculate the angle of displacement for the trunk. Using a .5-12 legged right triangle we solve for this angle. Using this angle and looking at the trunk, we know the tree will tip iff the center of mass lies past the furthest point of support so we can calculate L from the triangle by projecting a vertical line up from this point of support. L = 10/tan(2.4) ~ 240 so the answer is 2.4 meters.
Once the tree is tilting just B4 being toppled, the C.M. must be exactly above the hinge-point at the right of the drawing. At this position the tree is listing at an angle which has a tangent of 0.5/12(Pic.). The axe of the tree(on which the C.M is) makes too the same angle with a vertical line. In that situation it is not hard to show, that condition of the C.M. above the hinge point will require Lxtg(A)=0.1m Where A is the listing angle with tg(A)=0.5/x12
So from here L=0.1/tg(A)=0.1/(0.5/12)=2.4m
The perfectly symmetrical cylindrical tree has a uniformly distributed density in which the center of mass is in the middle of the tree. The chainsaw is forming an angle with the horizon in which this angle can be represented by t a n ( θ ) = a d j o p p . The o p p is the height of chainsaw, 0 . 5 c m and the a d j is the width of the tree minus the length of the chainsaw hence is 1 2 c m . Therefore t a n ( θ ) = 1 2 0 . 5 , the length L is the distance from the centre of the tree trunk to the center of mass, as the tree tips over the angle formed from the vertical will be equivalent to the angle that is lifting it. Hence the angle θ can be shown in terms of the length L and the distance from the center to the edge seeming as once this center of mass passes the point in which it is balancing, it will fall. Therefore t a n ( θ ) = L 1 0 , merging the two equation found and cancelling t a n ( θ ) we get 1 2 0 . 5 = L 1 0 . Solving for L gives us the answer of 2 4 0 c m , hence our answer in meters is L = 2 . 4 m .
Very well explained, even without drawings; good job!
Is it exactly 2.4m? Since the tree is already tilted a bit, the center of gravity must move 1 0 cos θ . The 10m is the hypotenuse, while the horizontal difference is actually a slight bit less.
Can someone maybe help in explaining "as the tree tips over the angle formed from the vertical will be equivalent to the angle that is lifting it"?
Log in to reply
Imagine the tree is cut horizontally through the base, if you lift up one side of the tree the other side will still be rested on the base and an angle will form from the horizon seeming as you are making a gap. This angle that forms is going to be the same angle that forms from the vertical with the side of the tree. I hope this helps clarify things.
Before the tree topples, the net torque on it is 0. Let θ be the acute angle between the slanted axis and the horizontal.
On the right side, the torque is mgL cos θ
while on the left side, the torque is mg(0.1) sin θ
cancel and balance the equation, we will get L=(0.1) tan θ
From the given diagram, we get tan θ = 0 . 5 2 0 − 8 =24
Substitute it into the equation and we get L=0.1(24)=2.4 metres
The pdf solution is posted at this link along with the figure
https://imgur.com/BzIZFph