Luogu P1004 - Square access

Computer Science Level 5

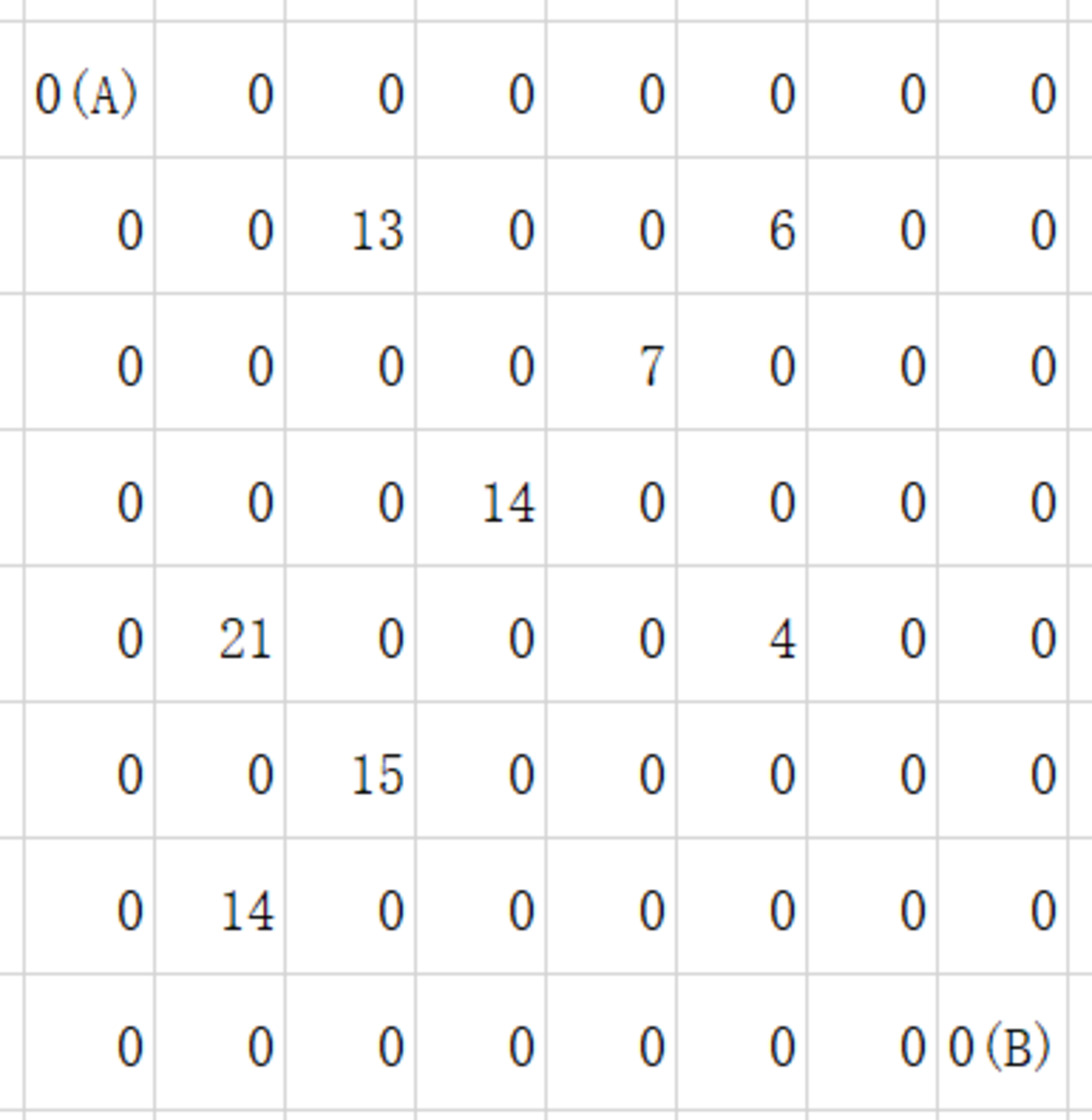
As shown above, the image shows a N × N N \times N square, and some of them have treasures. The number denotes the value of treasures.

A thief wants to get as many treasures as possible, in order not to be caught by police, he can only start from the square of the upper left corner A A , move rightwards and downwards without backing, to the square of lower right corner B B . Along the way on each trial, he can take away the treasure of the squares. Unfortunately, he only has two trials, that is, he will go from A A to B B twice. Notice that on the second chance, the treasures taken away on the first chance can't be taken again.

Given the size of the square, N N and the distribution of the values of treasures, find the maximum revenue the thief can get.

How to submit:

The pastebin below has 10 10 inputs. Each input has the format:

  • A number N ( 1 ≤ N ≤ 50 ) N (1 \leq N \leq 50) , the size of the square.

  • N × N N \times N numbers, the distribution of the values of treasures.

You should output: A number M M , the maximum revenue the thief can get.

Then submit the sum of all the outputs.

Inputs are here

Luogu Problem Set


The answer is 3756652.

Alice Smith by Alice Smith , 20, China

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Sahil Goyat
Dec 31, 2020 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
 
def op(A,n):                 
    l=[[[[-float('inf') if n in (i,j,k,m) else 0 for m in range(0,n+1)] for k in range(0,n+1)] for j in range(0,n+1)] for i in range(0,n+1)]
    l[n-1][n][n-1][n]=0
    for d in [[(k[0]-i,k[1]+i) for i in range(0,max(k)-min(k)+1)] for k in [(n-1,i) for i in range(n-1,-1,-1)]+[(i,0) for i in range(n-2,-1,-1)]]:
        for (i,j) in d:
            for (k,m) in d:
                l[i][j][k][m]=A[i][j]+A[k][m]*((i,j)!=(k,m))+max(l[i+1][j][k+1][m],l[i][j+1][k+1][m],l[i+1][j][k][m+1],l[i][j+1][k][m+1])
    return l[0][0][0][0]
s=i=0
with open('1004.txt','r') as f:
    r=f.readlines()
    while i<len(r):
        R=r[i][0:-1]
        if R.isnumeric():
            M=[[int(j) for j in k.split(' ') if j not in['',' ','\n']] for k in r[i+1:i+int(R)+1]]
            s+=op(M,int(R))
            i+=int(R)+1
        else:
            i+=1
print(s)

1 Helpful 1 Interesting 2 Brilliant 0 Confused

I couldn't understand your code.

But I'm trying the following: using dynamic programming, find the maximum treasure the thief can get on the first pass and which is the path he will make. then, set to zero the treasures that were taken that first path. again, using dynamic programming, find the maximum treasure on this new matrix. sum the treasures made in both cases

I still didn't got the correct answer. But I want to know if this logic is right.

asdasd asdasd - 4 months, 1 week ago

Log in to reply

No , its not correct I also tried it as my first attempt but it didn't work it looks like you have to run both runs simultaneously as the first thief knows that he will have a second chance which can affect his choice during the first run. In the many given inputs I have found that both methods give different results in some cases and same in some.. In my code I have run both runs at same time and used the fact that any given moment they will be on the same diagonal and then applied dynamic programming. see this example see this example here you can see that the sum of two max sums is less than the one optimized sum which covers all numbers

sorry for not writing comments in the code I am lazy ;)

Sahil Goyat - 4 months, 1 week ago

Log in to reply

Oh thanks! I'll take a second look at it

asdasd asdasd - 4 months, 1 week ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...