Mad Mirrors
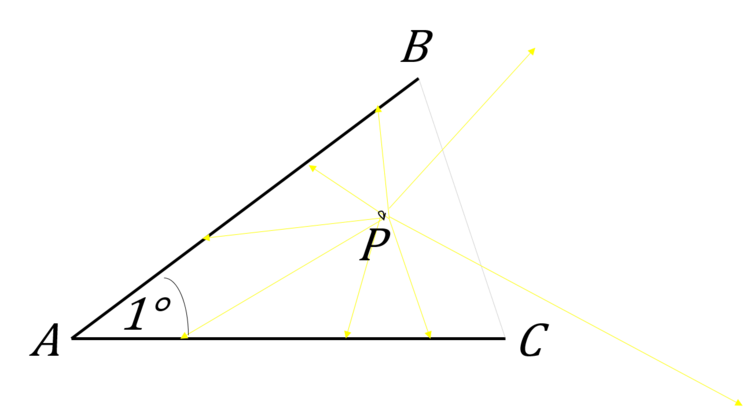 Two mirrors (represented by line segments in the plane) each have length 1 meter. They are joined such that one endpoint of one mirror coincides with one endpoint of the other mirror at the point
and such that the angle between the mirrors is 1 degree. Let points
and
be the remaining two endpoints which are not joined. A light source that emits light in all directions is placed at point
within triangle
. Find the maximum number of times a light ray can bounce off of
and/or
before intersecting
. (For example, one such light ray can bounce off of
, then
, then
again, then
again, then
again, and touch
; this light ray would have bounced off of
and/or
5 times.)
Two mirrors (represented by line segments in the plane) each have length 1 meter. They are joined such that one endpoint of one mirror coincides with one endpoint of the other mirror at the point
and such that the angle between the mirrors is 1 degree. Let points
and
be the remaining two endpoints which are not joined. A light source that emits light in all directions is placed at point
within triangle
. Find the maximum number of times a light ray can bounce off of
and/or
before intersecting
. (For example, one such light ray can bounce off of
, then
, then
again, then
again, then
again, and touch
; this light ray would have bounced off of
and/or
5 times.)
The answer is 180.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Note that if we reflect the triangle about line A B , then one reflection along line A B corresponds to one intersection with line A B (see the diagram if this is not clear to you.)
We can continue reflecting the triangle like this until it forms a circle:
Thus the problem becomes finding the maximum number of intersections of this light ray line with A B or A C . Clearly, since ∠ B A C = 1 ∘ , that there are 3 6 0 total reflected lines A B and A C . However, any drawn line can at most travel through half of them (shown above), so the answer is 3 6 0 ÷ 2 = 1 8 0 .