Magic Box Game
You're in a game show called "Magic Box," where you're given 4 identical balls to throw into 4 boxes randomly. Each box will earn you the point(s) written on it multiplied by the number of balls thrown into it. For example, if you put one ball into each box, you'll get 1 + 2 + 3 + 4 = 1 0 points.
What is the expected value of points earned from this game?
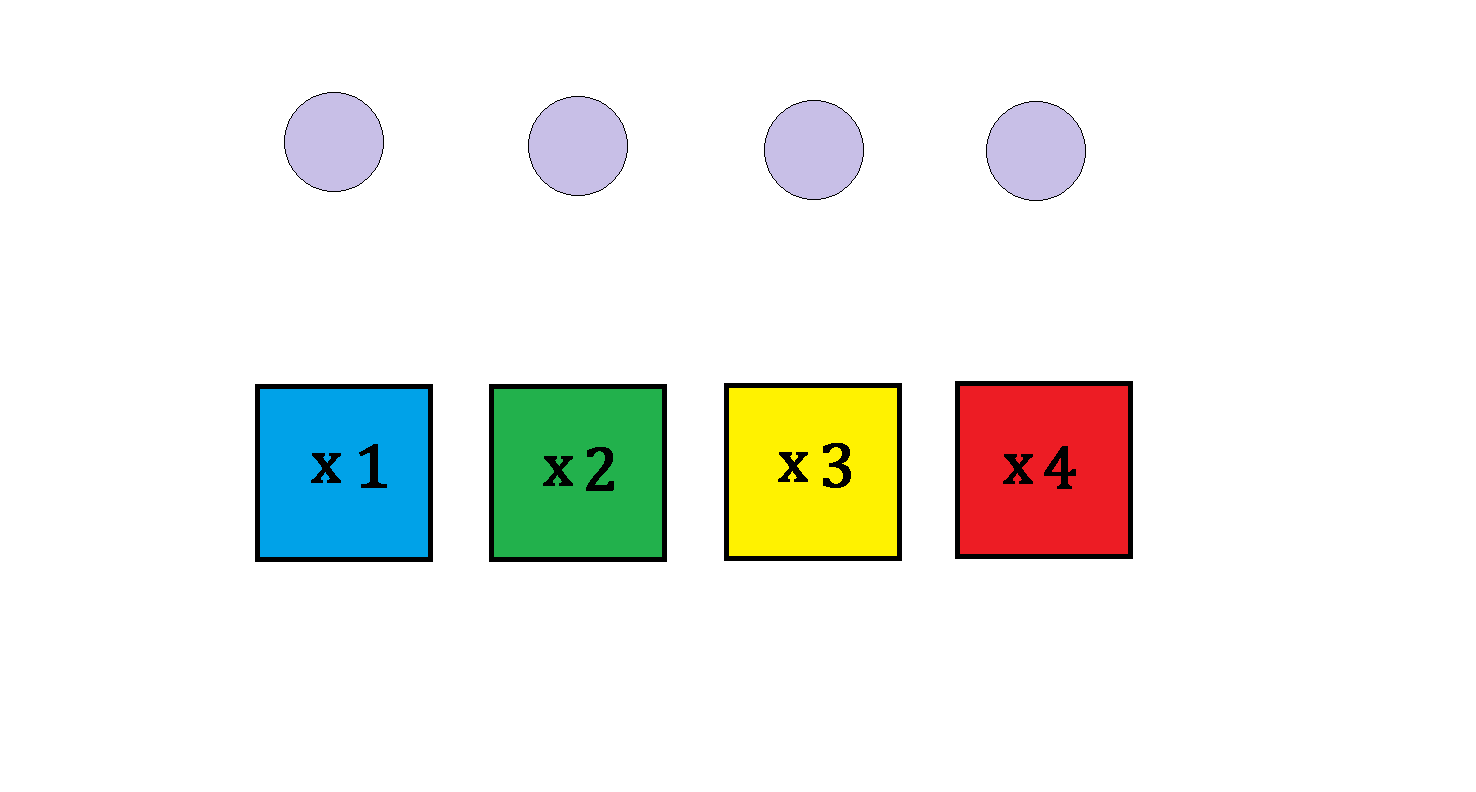
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Very nice and clean! 👍
brilliant idea out of the box keep posting.....
Relevant wiki: Central Limit Theorem
By putting 4 identical balls into 4 different boxes, the total combinations will equal ( 4 4 + 4 − 1 ) = ( 4 7 ) = 3 5 ways according to Stars & Bars Equation , and we know that the lowest possible points equal to 4 while the highest being 1 6 .
By using partition, we will see that there is only one way to earn 4 points: 1 + 1 + 1 + 1 = 4 .
And there are 5 ways to earn 1 0 points: 1 + 1 + 4 + 4 = 1 + 2 + 3 + 4 = 2 + 2 + 3 + 3 = 1 + 3 + 3 + 3 = 2 + 2 + 2 + 4 .
Now by going for all partitions, we will obtain expected value = 3 5 ( 4 + 5 + 1 5 + 1 6 ) × 1 + ( 6 + 1 4 ) × 2 + ( 7 + 1 3 ) × 3 + ( 8 + 9 + 1 1 + 1 2 ) × 4 + 1 0 × 5 = 1 0 3 5 0 = 1 0 .
Alternatively, by using Central Limit Theorem , the distribution of the point combination will form a bell-like curve of normal distribution as the following:
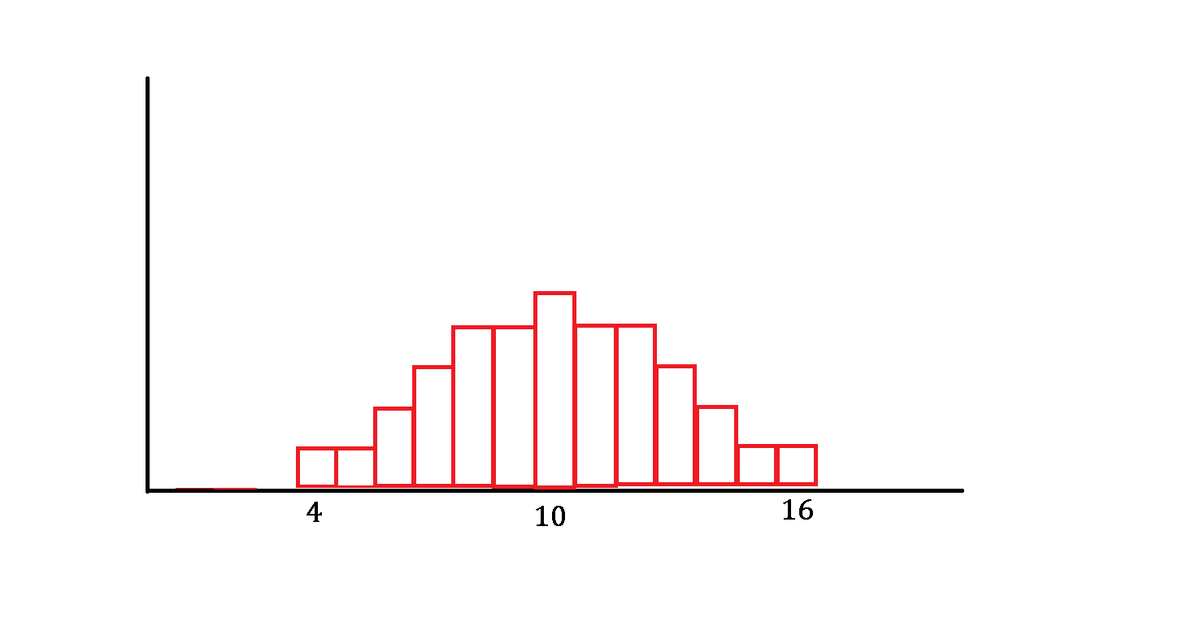
From this distribution graph, we can depict the expected value or average = 1 3 4 + 5 + 6 + . . . + 1 4 + 1 5 + 1 6 = 1 0 , which is the mean μ in the normal distribution.
Therefore, the expected score of this game is 1 0 points.
This sum can be solved by linearity of expectation. We have four independent random variables X 1 , X 2 , X 3 and X 4 , denoting the reward from throwing ball 1, ball 2 ball 3 and ball 4 respectively. We want E [ X 1 + X 2 + X 3 + X 4 ] , which is same as sum of expectations of X i by linearity. Hence the answer is 4 × 2 . 5 = 1 0
thanks bro... great solution...
1 + 2 + 3 + 4 = 10. Since you have to throw all four, well . . . That sounds like a pretty boring game show!
Welcome back to Ten in the bank! where we give you ten thousand no matter what!
[This solution is to be edited]
The minimum sum of these numbers is 4 (1 4) and the maximum could be 16 (4 4). However the probability of each of these sums occuring is not distributed equally ( hence is not 1 3 1 .
Highest possible value from throw= 4*4= 16 (when all the balls are thrown in the highest value box)
Lowest possible value= 1*4= 4 (when all the balls are thrown into lowest value box)
Average= (4+16)/2= 10
average of 1,2,3,4 = 2.5 so expected value of 1 throw is 2.5 pts. So the expected value of 4 throws is 2.5*4= 10 points .