Magic Hexagon Starting With 0

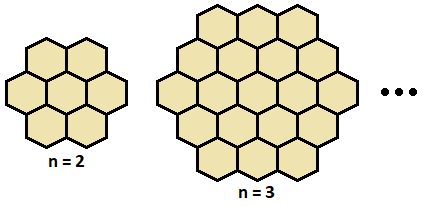
The number of hexagons in a grid of side $n$ is $3n(n-1)+1$ , so the sum of numbers from $0$ to $3n(n-1)$ is $\tfrac32n(n-1)(3n^2-3n+1)$ , and so the magic number should be $\frac{3n(n-1)(3n^2-3n+1)}{2(2n-1)} \; = \; \frac{3[(2n-1)^2 - 1](3(2n-1)^2 + 1]}{32(2n-1)}$ Since $2n-1$ and $[(2n-1)^2-1][3(2n-1)^2+1]$ are coprime, we see that $M$ is an integer only when $2n-1$ divides $3$ , so when $n=2$ .

If $n=2$ then since neighbouring edge hexagons sum to the magic number $M=7$ , any two non-consecutive edge hexagons must be equal to each other. Thus the seven hexagons cannot be filled with seven distinct numbers, so the case $n=2$ is not possible, either.

There is no value of $n \ge 2$ for which a $0$ -based magic hexagon is possible.