Digits and Years
The year 2011 has the property that the year plus the sum of its digits is equal to 2015, since 2 0 1 1 + ( 2 + 0 + 1 + 1 ) = 2 0 1 5 . Find the only other year with this property.
The answer is 1993.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Brilliant, thanks for the solution
1 2 3 4 5 |
|
It is easy to verify that none of the years from 2000 onward will work and when you try 1999 it will be 1999+28 =2027
that mean its 12 more than 2015 so we will need to sum it from 2027
but if you decreased any from that year or the sum of its digits the other will be decreased by one in the 9 times after 1999
so you sum (12/2) from each
so 1999-6 =1993
1+9+9+9-6 =22
1993+22 =2015
sorry for my english and because its not a general solution
excellent solution
I don't get questions like this that are easier/faster to do by hand than by a formula. Just count every year less than 2011 until you get the right answer 1993... takes 2 minutes tops.
10 for a=0 to 2
20 for b = 0 to 9
30 for c = 0 to 9
40 for d = 0 to 9
50 let x = 1001 a+101 b+11 c + 2 d
60 if x = 2015 then print a;b;c;d
70 next d
80 next c
90 next b
99 next a
Pseudocode
Meanwhile, 5 minutes ago....everyone else got it already.
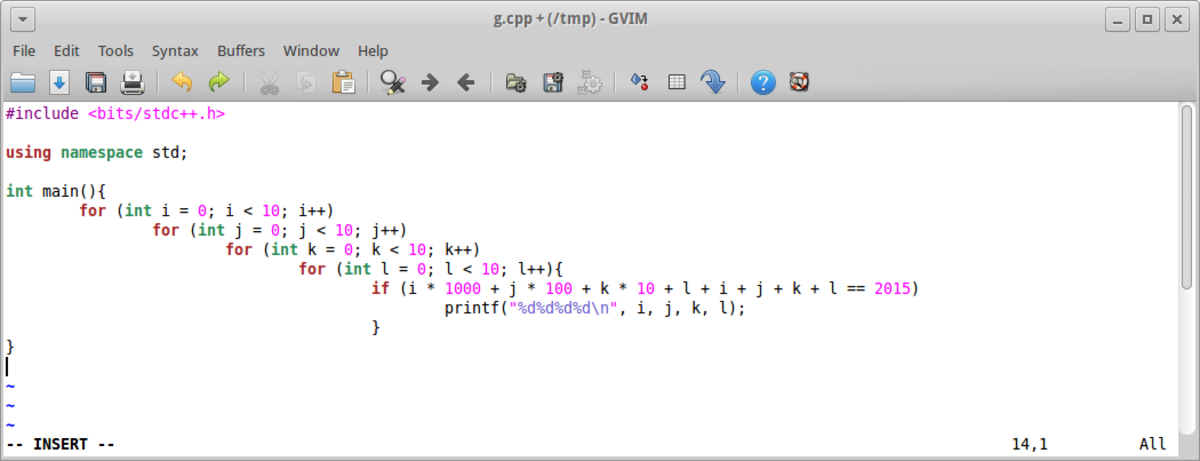
It is easy to verify that none of the years from 2000 onward will work, so let's check in the 1900s. There are many ways to go about this search that will work. Here's one possible approach:
If the year is 1 9 A B where A and B are digits, then we need 1 9 0 0 + 1 0 A + B + ( 1 + 9 + A + B ) = 2 0 1 5 . This simplifies to 1 1 A + 2 B = 1 0 5 . Since 2 B ≤ 2 ⋅ 9 = 1 8 , we must have A = 9 , which gives B = 3 .
Thus, 1993 is the other year that satisfies this property, with 1 9 9 3 + ( 1 + 9 + 9 + 3 ) = 2 0 1 5 .
Remark: It is easy to show that no earlier century could work since the largest sum of digits for a four digit number is 4 ⋅ 9 = 3 6 , so the year must be at least 2 0 1 5 − 3 6 = 1 9 7 9 .