Magic Pyramid
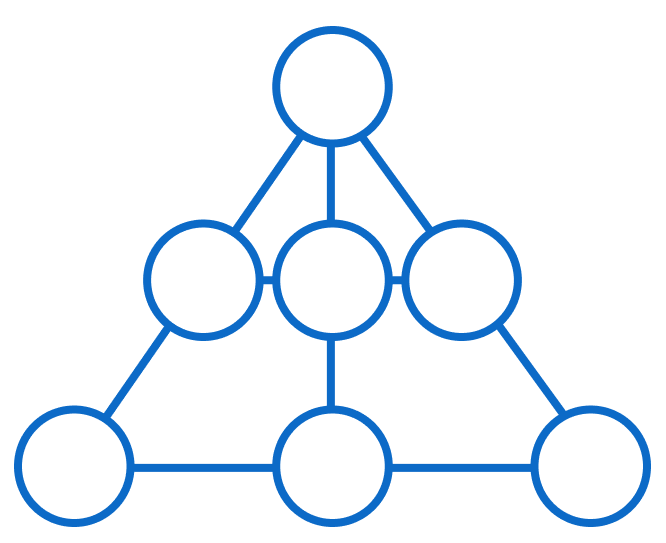
Place the digits 1 through 7 in the circles, each only once, such that any trio of digits on the same line will add to the same number.
While there are multiple solutions, only one digit can go in the top circle. Which one?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The sum of all the numbers from 1 to 7 is 2 8 . If n is the number at the top, then 2 8 − n must divide by 3 , since the the remaining two circles of the three lines joined by the top circle must add up to the same numbers.
This implies that n = 1 , 4 or 7 .
Also 2 8 − n must be even, since the two horizontal numbers must add up to the same number.
That leaves, n = 4
It remains to show that we can achieve the conditions of the problem with n = 4 . Indeed we can:
2 6 4 3 5 7 1
Can you show that such a configuration is actually possible, preferrably by providing one?
Another way to get to n = 4 directly would be to count in how many lines each circle appears. We see that every circle is in 2 lines except for the top circle which appears in 3 lines. That means the sum of all the circles of all the lines respectively is 2 × 2 8 + n = 5 6 + n with n as the number on the top. This number must be divisibe by 5 as there are 5 lines. Hence n can only be 4.