Magic square - 1.0
The figure below shows a
magic square.
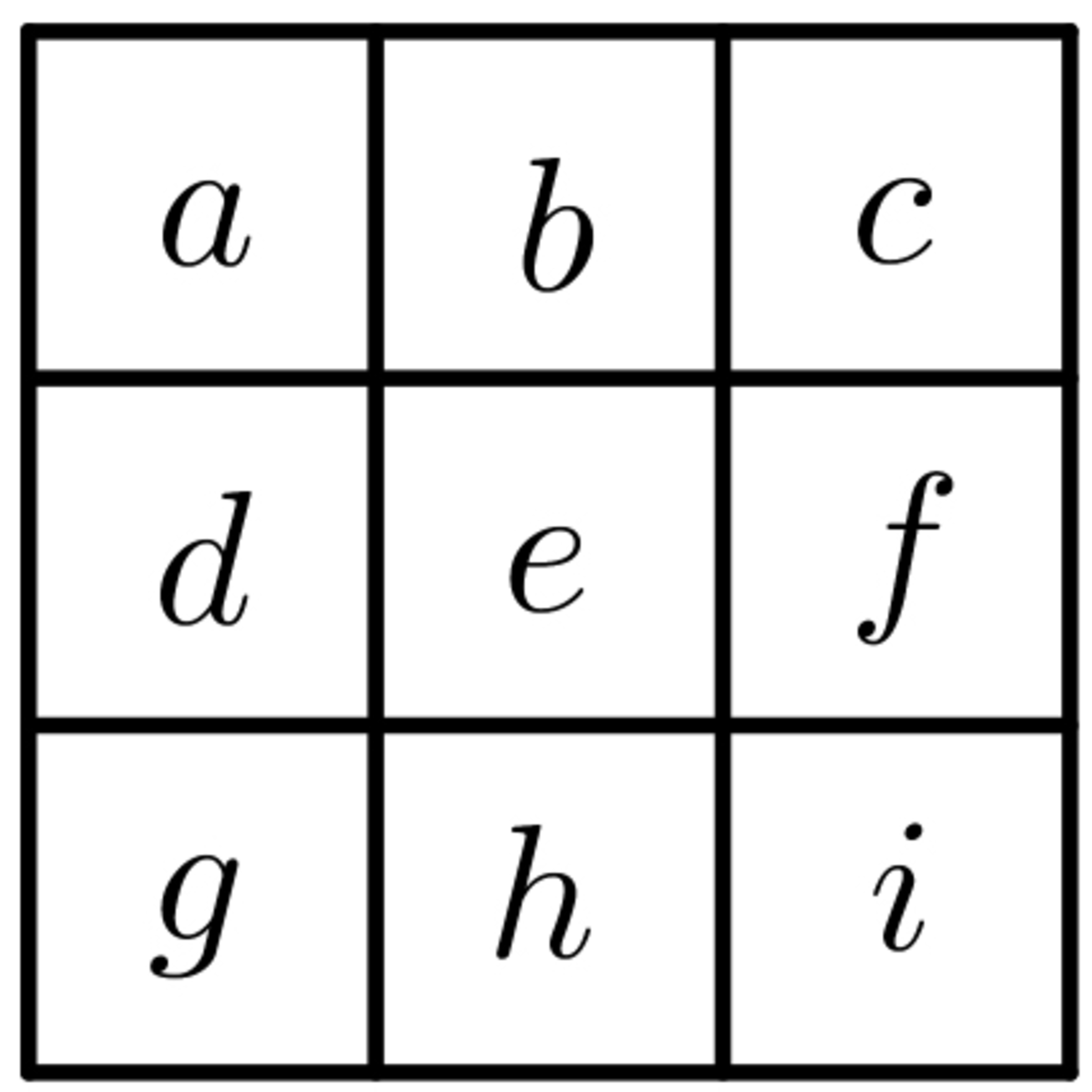
Which of the following statements is/are true?
A : It is possible that ( ) are in some order.
B : It is possible that ( ) are in some order.
Note:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A : The sum of the numbers is 2 9 , which is not divisible by 3 . Since the 2 , 2 , 3 , 3 , 3 , 4 , 4 , 4 , 4 numbers are intgeres, it is not possible.
B : Suppose yes. Then a + b + c = d + e + f = g + h + i = a + d + g = b + e + h = c + f + i = 3 0 + 1 + 2 + 4 + 5 + 7 + 8 + 1 0 + 1 1 = 1 6 . It is celar that since 1 0 + 1 1 > 1 6 , 1 0 and 1 1 can't be in the same row or in the same column. There are two ways to add two numbers to 1 1 to get 1 6 : 1 6 = 1 1 + 0 + 5 and 1 6 = 1 1 + 1 + 4 . There are two ways to add two numbers to 1 0 to get 1 6 : 1 6 = 1 0 + 1 + 5 and 1 6 = 1 0 + 2 + 4 . But 2 and 4 can't be in the same row/column, which is contradiction. So it is impossible.
Therefore neither of them is possible.