Magic Square - Only Corners
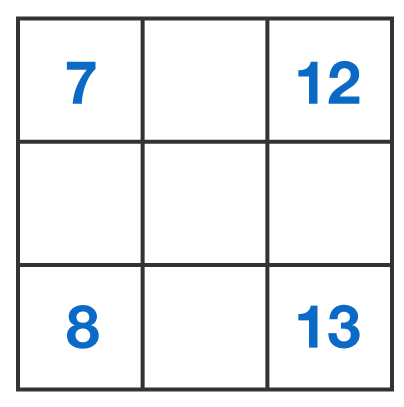
In the 3 × 3 magic square above, each row, column or diagonal sums up to the same value.
What is this value?
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
When I first set up the question, I forgot that the diagonals had to have the same sum. That resulted in an unsolvable magic square lol.
An interesting lead-on is "What is the minimum number of squares that we have to provide in order to uniquely solve the magic square?" Any thoughts?
We have 8 equations (with 1 repeated, so in essence 7) and 10 unknowns (inclusive of the sum). Supposedly if we provide 3 unknowns we can uniquely solve the system, but I can't see how to do this. Maybe there are more repeated equations?
Log in to reply
It is easy to solve a 3×3 magic square, if we either have all 3 numbers in the same column/row (then we have the sum as well) or we have two numbers in the same column/row and the middle number (as it is easy to prove, that the sum is always 3 × the middle number).
Can you find the solution in these cases?
What can you do if the position of the numbers we know is different from those in the cases described above?
Log in to reply
I post a new discussion to talk about this.
What you said made a lot of sense, and I think i'm seeing where my missing equation went.
The following Lemma is easy to prove, and can be used for future easier magic square problems to simplify them quite a bit.
Lemma : The magic sum in a 3x3 magic square is equal to three times the number in the centre square.
Proof : Let the Magic Sum be S and the number in the centre be x ,
Sum up the numbers in the two diagonals, the middle column and the middle row. This is equals to 4 S .
Notice that this is also equal to all the numbers once plus three times the middle number which has a sum of 3 S + 3 x
Which implies 3 S + 3 x = 4 S , S = 3 x
it is easy to see that
( 7 + 1 3 + x ) = 3 x and x = 1 0 , 3 x = 3 0
QED(?):)
Great use of that lemma! I remembered it after posting this problem, and applied it to a different scenario.
Well, the elements of diagonal are in AP 2x= 7+13=20, x=10, Common sum=30
If ye want I can prove the diagonal elements are in AP in a magic square of order 3
There are 9 numbers, 4 provided which give a margin of 7-13, 2 numbers short. As all numbers are consecutive there must be either 5, 6, 7, 8, 9, 10, 11, 12,13 or 6, 7, 8, 9, 10, 11, 12, 13, 14 or 7, 8, 9, 10, 11, 12, 13, 14, 15.
In comparison: 5+6+7+8+9+10+11+12+13 = 81, which is an average of 9 p/ square which counts to 27.
6+7+8+9+10+11+12+13+14 = 90, 10 p/ square = 30.
7+8+9+10+11+12+13+14+15 = 99, 11 p/ square = 33.
As 12 + 13 is 25 and the options are 27, 30 and 33, 27 is eliminated needing a 2.
As 7 + 8 = 15, the remaining options 30 and 33, 33 is eliminated needing 18.
Therefore, the only option left is 30.
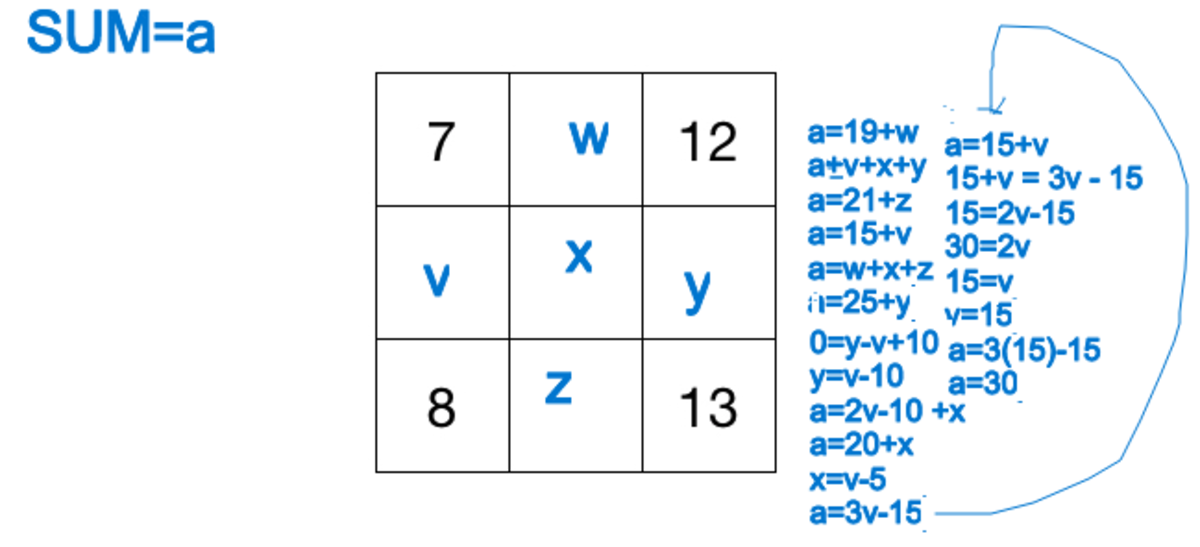
Let's call our sum S, and the missing values of the 1st, 2nd and 3rd row of the middle column a, b and c, respectively.
Then take the sums of the 1st and 3rd rows and the main diagonal:
S = 7 + a + 12 = a + 19
S = 8 + c + 13 = c + 21
S = 7 + b + 13 = b + 20
Now, if we add these 3 equations together, we get:
3S = (a + b + c) + 60
The sum of the middle column is:
S = a + b + c
if we take away this from our previous sum, we get:
2S = 60
S = 3 0