Magic Squares
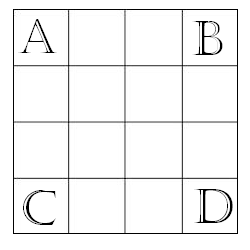
A magic square of order 4 is created by putting the integers 1 to 16 into a 4 by 4 square grid so that the sum of the numbers in each row, column and main diagonal is the same. What is the sum of the integers at the corners of this magic square (labeled by letters as shown above)?
The answer is 34.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
we know that if the sum of elements all rows , collums and diagonals are x then the sum of all the corner elements are also the x for square matrix. Here sum of all numbers i.e 1+2+3...+16 = 136 so x = 136 / 4 = 34 so ans is 34
Log in to reply
The rows would add up correctly but the columns would not...
Nice solution! :D
By the way, I just want to ask why this problem rose very rapidly from Level 1 to Level 4? I really doubt of the level of this problem. Thanks in advance. :)
Log in to reply
I agree...I liked this problem a lot but it is definitely not one of the harder ones I have solved......I have absolutely no clue about this sudden rating jump...
It is only stated that the main diagonal has the same sum as rows and columns. You considered that both main and second diagonal have the same sum (by telling that C+L+I+B=34) but you didn't prove that the soulution exists if you do so (maybe there is no such configuration so that both diagonals have the same sum as rows and columns). Can you please explain it if you have the proof for that?
Log in to reply
It states that "each row, column and main diagonal" have equal sums, meaning that each main diagonal has that sum, not just one of them.
note that the answer is exactly the one-fourth of the sum of all the nos. from 1 to 16.
I have done by similar way
nice..
there are 16 numbers from 1 to 16, it can be easily inferred that sum of all numbers (1+2+3+.......16)=136........since there are four rows so sum of each row or column is 136/4=34. Now accordingly we can arrange the numbers in the squares.....
You have done it in a very simple method Very good
ohhhh... i get it know.
| 7 | 1 | 16 | 10 |
| 2 | 12 | 5 | 15 |
| 14 | 8 | 9 | 3 |
| 11 | 13 | 4 | 6 |
7+10+11+6=34
wheres the fun in algebra? just sit there for an hour and make it up because its harder to do like that.
That's awesome, I couldn't get the diagonals right(38) 😕
Me also can’t find the diagonals right (32), how to decided the placement of all those number?
There's a few ways to do it: 01-15-14-04 12-06-07-09 08-10-11-05 13-03-02-16 ...also works.
I think this one will also fulfil another condition i.e. the four numbers in a each of the four corner squares will also add up to 34.
I didn’t understand the question, I thought you had to fill in the numbers 1 to 4.
I got the answer in first minute. But i couldn't get the diagonals right.
Label all the numbers in the magic square be x 1 , x 2 ,...., x 1 6 . The magic constant is 2 1 n ( n 2 − 1 ) = 34. Then we have x 1 + x 2 + x 3 + x 4 + x 1 3 + x 1 4 + x 1 5 + x 1 6 = 6 8 ( x 1 + x 4 + x 1 3 + x 1 6 ) + ( 6 8 − ( x 6 + x 7 + x 1 0 + x 1 3 ) = 6 8 ( x 1 + x 4 + x 1 3 + x 1 6 ) + [ 6 8 − { 6 8 − ( x 1 + x 4 + x 1 3 + x 1 6 ) } ] = 6 8 2 ( x 1 + x 4 + x 1 3 + x 1 6 ) = 6 8 x 1 + x 4 + x 1 3 + x 1 6 = 3 4 And from question, { x 1 , x 4 , x 1 3 , x 1 6 } = { A , B , C , D } . Therefore, A + B + C + D = 3 4
there is an error in your formula...it is n/2( n^2 +1)
Log in to reply
The sum of the first n integers is n(n+1)/2 = 16(17)/2=8(17) = 134
Sum=n(n^2+1)/2 where n=the number of rows and columns in our case sum=4×(16+1)/2 = 34
You have done the sum in a very complicated method. It can be done very simply
I took the first four intergers, 1, 2, 3, and 4, added them together to make 10, took the last four intergers, 16, 15, 14 and 13, added them together to make 58. Found the mid point between 10 and 58 which is 34. :)
Lowest even numbers 2+4=6 highest odd numbers 13+15=28 Added together 6+28=34
add 16+15+14+13+12+11+10+9+8+7+6+5+4+3+2+1 = 136 this will gives u the total sum of the solution. then this number will divided by 4 we will get 34.
I have a solution. We know each row adds up to the same number. So, the number should be 1+2+3+4+5+......+16=136. This number is divided by 4 which gives us 136/4=34(actually, I just sat and tried to fill all the grids but failed everytime but the sum of the numbers always added up to 34, my dad explained me the logic behind it) Now, we know that each row, column and diagonal adds up to 34. So, here, any two numbers in, let's say, a row adds up to 1/2 of 34 which is 17. I considered the two numbers to be A and B(first row) and C and D(last row). So A+B=17 and C+D=17. Adding, we get A+B+C+D=34.
To know more on magic squares see https://youtu.be/-czqJpGGQck. Jump to 14:50 for 4X4 Square.
We can divide up the square like this:

Let s = A + B + C + D denote our desired sum of corners, and r , g and b denote the sums of the red, green and blue shaded regions, respectively. From the problem description, we can directly infer that the total sum of the square s + r + g + b = 1 + 2 + 3 + ⋯ + 1 6 = 1 3 6 . This also means that each line sums up to 4 1 3 6 = 3 4 . By adding the sums along all of the colored lines, we arrive at the following equation:
( s + r ) + ( s + g ) + ( s + b ) = 6 ⋅ 3 4 = 2 0 4
We can solve this equation by substituting the total sum: ( s + r ) + ( s + g ) + ( s + b ) = 2 0 4 2 s + ( s + r + g + b ) = 2 0 4 2 s + 1 3 6 = 2 0 4 2 s = 6 8 s = 3 4
I thought that it might be only a verbal trick, so there are 4 numbers in each row, column or diagonal (4 squares) so i just arranged the numbers in order so the corner numbers will be (1+4+13+16=34) lol maybe i got lucky or smart i don't know please tell me if I'm wrong :D
Using Gauss' addition technique, the sum of 1 through 16 becomes (1 + 16) + (2 +15) + (3 + 14) + ... which translates to 17 x 8 = 136 Dividing 136 by 16 yields an average value per square of 8.5 therefore any four symmetrically placed squares will have a sum of 8.5 x 4 = 34
1 15 14 4
12 6 7 9
8 10 11 5
13 3 2 16 is a solution,so 1+4+16+13=34
Line one 04 14 15 01 Line two 09 07 06 12 Line three 05 11 10 08 Line four 16 02 03 13 This is magic square use 1 to 16 numbers
A magic square of order 4 is a matrix:
[a(i,j)], i, j = 1,2,3,4; with:
a(i,j) ∈ {1,2,3,...,4^2}; with the properties:
Σ{i = 1; 4 (a(i,j))} = M(4); j = 1,2,3,4;
Σ{j = 1; 4 (a(i,j))} = M(4); i = 1,2,3,4;
Σ{k = 1; 4 (a(k,k))} = M(4);
Σ{k = 1; 4 (a(k,(4 - k + 1)))} = M(4);
ΣΣ{(i = m; m + 1)(j = p; p + 1)(a(i,j))} = M(4); m = 1,2,3; p = 1,2,3;
Sum(n) = ΣΣ{(i = 1; 4)(j = 1; 4)(a(i,j))} =
Sum(n) = Σ{(k = 1; n^2)(k)} = n^2(n^2 + 1)/2; for n = 4:
Sum(4) = 4^2(4^2 + 1)/2 = 136; it can be show that:
M(n) = Sum(n)/n = n(n^2 + 1)/2; (MAGIC NUMBER), for n = 4:
M(4) = 4(4^2 + 1)/2 = 34;
if we denote:
A = a(1,1); B = a(1,4); C = a(4,1); D = a(4,4);
E = a(2,2); F = a(2,3); G = a(3,2); H = a(3,3);
we have:
ΣΣ{(i = 2; 3)(j = 2; 3)(a(i,j))} = M(4) = E + F + G + H; (1)
Σ{k = 1; 4 (a(k,k))} + Σ{k = 1; 4 (a(k,(4 - k + 1)))} =
A + B + C + D + E + F + D + H = M(4) + (M(4) = 2M(4); (2)
substituting (1) in (2), we have:
A + B + C + D + M(4) = 2M(4);
A + B + C + D = M(4) = 34. (ANSWER)
Solution 1: For a 4x4 magic square the sum of rows/columns/diagonals is [1+2+...16]/4 i.e. 34. This is going to be the sum of the numbers in any proper closed shape.
Solution 2: Now for a 4x4 magic square the jump number is 4. If we start with 1 then jump 4 numbers and land on 6. Then once again jump 4 numbers & land on 11. Then once again jump 4 to get 16. Now add those numbers i.e. 1 + 6 + 11 + 16 == 34. This has worked for me for a very long time!
Well the #ANSWER is 34 but for how to create a magic square of order 4 .
You can go to Fourth-order Magic Squares
Note that there are many types of magic squares having integers 1 to 1 6 that can be constructed. But the sum of the vertex numbers is always 3 4 .
Proof? :)
And what will be the sum of numbers in case of 3*3 magic square having number 1 to 9.
Log in to reply
use the formula for finding the magic constant
M = 2 n ( n 2 + 1 ) , where n=3
so, the sum of numbers of any column/row/diagonal=M=15
45 for the entire square, 15 for any row or column, the sum of the four corners varies depending on number placement.
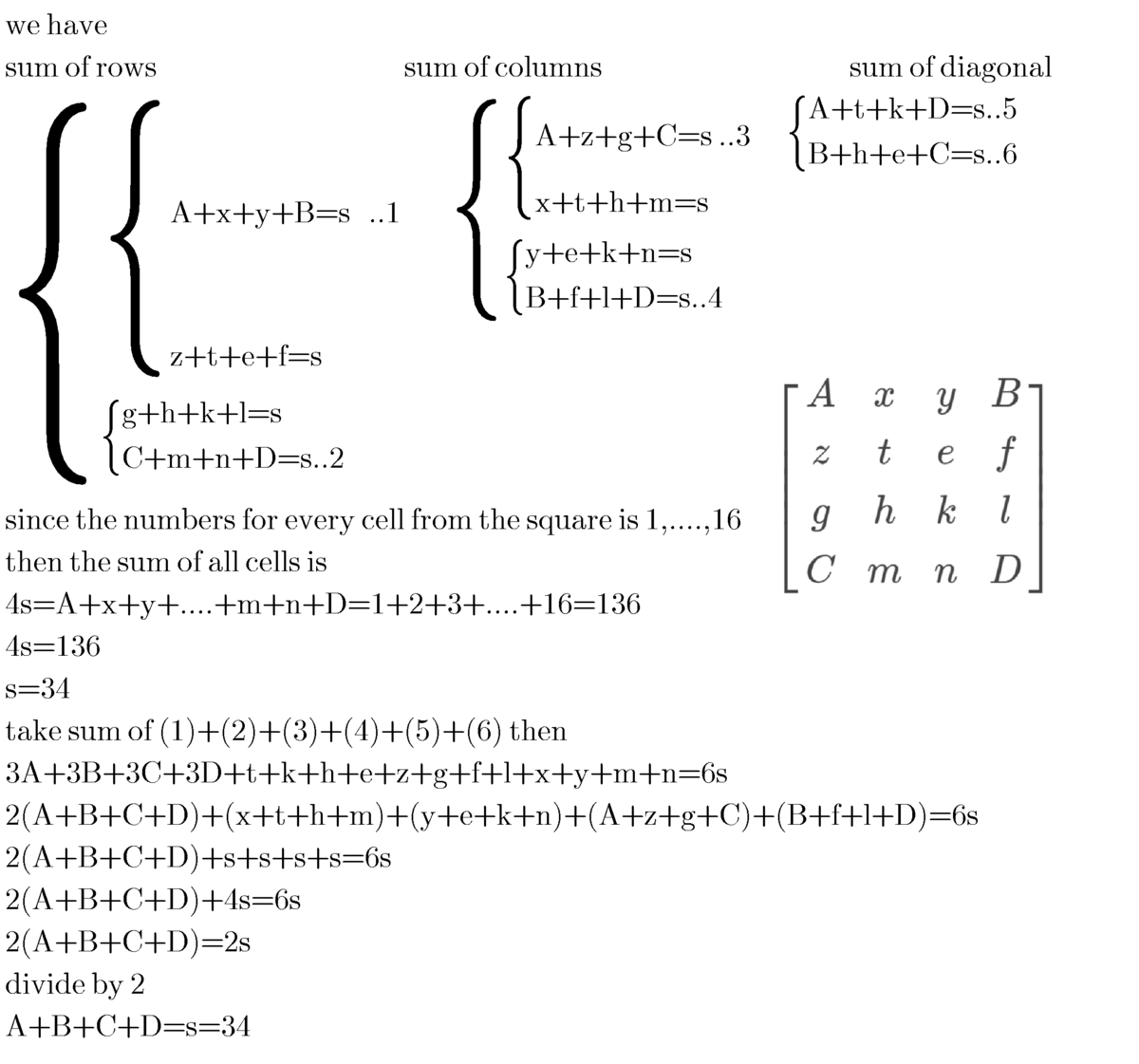
In a magic square of order 4, we are filling in numbers from 1 to 16.
So, sum of all the numbers=1+2+3....16=136
which gives us, sum of numbers in a row, column or diagonal= 136/4=34
A G E H F I B J
K C L O M P N D
let this be the magic square of order 4
then, A+H+M+D=34
C+L+I+B=34
A+E+F+B=34
C+O+P+D=34
adding all the above equations, we get
2A+2B+2C+2D+H+M+L+I+E+F+O+P=34+34+34+34
2(A+B+C+D) + (H+L+E+O)+(F+I+M+P)=4X34
2(A+B+C+D) + (34)+(34)=4X34
2(A+B+C+D)=2(34) WHICH GIVES US A+B+C+D=34.