Magic table

We can count that $j+e = 55 - 21 - 21 = 13$ . So we have 4 cases to study:

1. $d+f = 21-3 = 18$ we cannot make this sum without using each number more than once.

2. $d+f = 21-4 = 17$ then $d+f = 10 + 7$ and $a+i = 12$ , but we cannot make 12 without using each number more than once.

3. $d+f = 21-5 = 16$ , then $d+f = 10 + 6$ or $d+f = 9 + 7$ . If $d+f = 10 + 6$ , then $a+i = 9+4$ and $b+c=2$ , but we cannot make sum 2 from the given numbers without using each number more than once. If $d+f = 9 + 7$ , then $a+i = 10+3$ and $h+g=11$ and we cannot make the sum 11 without using each number more than once. If $a+i = 3+10$ , then $b+c=h+g=4$ and we cannot achieve that without using each number more than once.

4. $a+i = 21-7=14$ . If $a+i = 10+4$ , then $d+f = 15$ , but we cannot make this sum without using each number more than once. If $a+i = 9+5$ , then $d+f = 15$ , but we cannot make this sum without using each number more than once.

Therefore it is impossible to construct the table where $S = 21.$

The sum of the numbers $1$ through $10$ is $55$ , and by using the totals $21\times4=84$ , we can work out the sum of the corners with $84-55=29$ .

As either column uses three numbers including two corners, we cannot have three corners adding up to $21$ , otherwise we would wind up with a duplicate number in the centre of one of the columns. this means none of the corners can be $8$ , as the other three corners would total $21$ .

This leaves us with two possible sets of corners:

1. $10,9,6,4$
2. $10,9,7,3$

With set 1:

We cannot have columns of $6,4$ (as it would require an $11$ tile) or $6,9$ (as it would require a second $6$ tile). This leaves us with the columns $6,10$ and $9,4$ . With these, we cannot have the row $10,9$ (as that would require two $1$ s), so we are left with rows $10,4$ and $6,9$ . However with this, a $5$ is needed for the $10,6$ column, but to complete the $6,9$ row, we'd need either $1+5$ or $2+4$ , both of which use duplicate numbers. This means this set will not work.

With set 2:

We cannot have rows of $10,9$ (as again that would require two $1$ s) or $10,7$ (as that would need either two $2$ s, or $3+1$ which has a duplicate $3$ ). This leaves us with rows $10,3$ and $9,7$ . However, we cannot have columns $7,3$ (as again it would require an $11$ tile), or $9,3$ (as it would require a duplicate $9$ ). This means that this set also does not work, therefore it is impossible to fill such a table where the sum of every side equals $21$ .

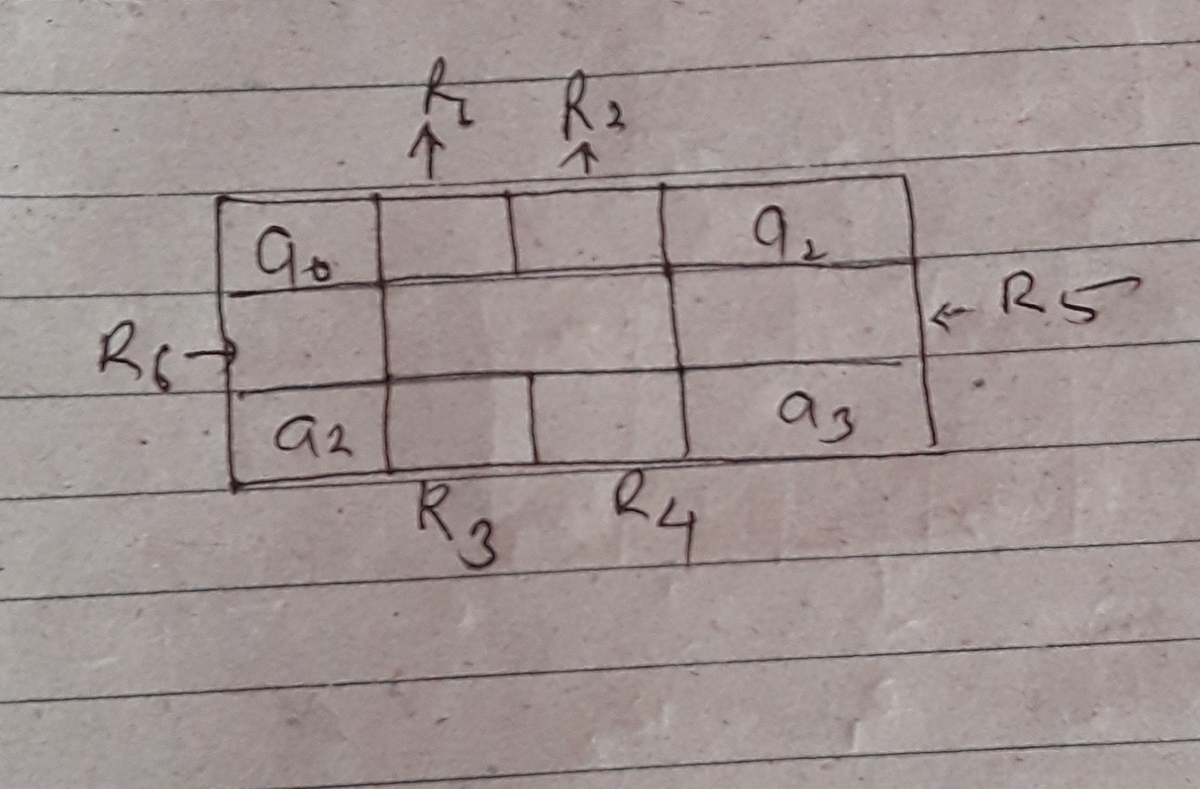
Since the sum of 1st 10 natural number is $55$ and each case we observe that $a_0,a_1,a_2$ and $a_3$ are added twice along row and column addition. We can observe that $\small \text{diff. is of 4}\begin{cases} 17 =18\times 4-55 \\ 21 =19\times 4 -55 \\25= 20\times 4 -55 \\ {\color{#3D99F6} 29 = 21\times 4-55 }\\33 = 22\times 4 -55\end{cases}$ Note that $a_0+a_1+a_2 +a_3 =29$ so 3 of them should have the same parity (also a big as possible, if not, then one of them can result to 2 digit number greater than 10) and 4th one should have opposite parity.

---

Let take some examples

If $\,(a_0,a_1,a_2)= \,(9,{\color{#3D99F6}7}, 5)$ then $a_3 = 8$ . Also note that $a _0 + a_3 + R_6 =21 : R_6 = {\color{#3D99F6}7} = a_1$ which is false.

If $\,(a_0,a_1,a_2) =\,(10,8,6)$ then $a_3 = 5$ also $R_6 =5$ which is again false

---

So from here we can conclude that if $\,(a_0,a_1,a_2),\,(a_0,a_2,a_3),\,(a_1,a_2,a_3)$ belongs to same parity then $\,(a_3, a_1 , a_0)$ will be of opposite parity which is same as any of $\,(R_1,R_2.....,R_6)$ . Hence, the sum $21$ is not possible with all distinct number from 1 to 10.

Here is a brute force approach using $Mathematica$

Select[Permutations@Range@10,Tr@#[[1;;4]]==21&&Tr@#[[4;;6]]==21&&Tr@#[[6;;9]]==21&&#[[9]]+#[[10]]+#[[1]]==21&]

this code checks all tuples and returns {} which means, no such tuple exists

7 possible triples that sum to 21 for the vertical sums: {(10,9,2)(10,8,3)(10,7,4)(10,6,5)(9,8,4)(9,7,5)(8,7,6)}

Only three pairs of these triples don't repeat numbers.

(10,9,2) and (6,7,8) have corners that sum to 26. These with the remaining digits (1,3,4,5) sum to 39, not 2*21=42 for the horizontal sums.

(10,8,3) and (5,7,9) have corners that sum to 27. These with the remaining digits (1,2,4,6) sum to 40, not 2*21=42 for the horizontal sums.

(10,6,5) and (4,8,9) have corners that sum to 28. These with the remaining digits (1,2,4,6) sum to 41, not 2*21=42 for the horizontal sums.

So none of the pairs of vertical sums are compatible with the pairs of horizontal sums.

By understanding that there is only a certain amount of solutions, you can logically guess that in the other tables the numbers were arranged in a pattern close to a new one you would make. So that in each row there could be a certain possibility of the placement of the numbers. So you could guess the answer without any math involved.

I found the following (and above) sum sequences resulting in 21 that would dovetail with one another: 10 + 3 + 8, 8 + 4 + 2 + 7, and 7 + 9 + 5; the remaining numbers would be 6 and 1, and the only available possibilities with which to add them would be a (3 or 10) and a (9 or 5), neither of which would assist in equaling 21.

Another example: 7 + 3 + 2 + 9, 9 + 8 + 4, and 4 + 1 + 6 + 10, with the remaining digit 5, which could only be added to 10 and 7, which again does not equal 21.

Based on the above examples, I determined that it was very, very unlikely for there to be a solution resulting in all sums equaling 21 and connecting in the way described.

Other possible sums resulting in 21 include: 4 Digit Sums: 1 + 3 + 8 + 9; 1 + 4 + 7 + 9; 6 + 4 + 3 + 8; 2 + 6 + 3 + 10; 3 Digit Sums: 6 + 10 + 5

Note that $1+2+3+…+9+10=55=(a_1+a_2+a_3+…+a_9+a_{10})$ .

Let the corners be $a_1, a_2, a_3, a_4$ and the rest $a_5, …, a_{10}$ . If we sum the rows and columns we get that $[2*(a_1+a_2+a_3+a_4)]+a_5+a_6+a_7+a_8+a_9+a_{10}=84$ . Thus, $a_1+a_2+a_3+a_4=29$ . Therefore $a_5+a_6+a_7+a_8+a_9+a_{10}=84-29-29=16$ . But, if we sum up the lowest 6 integers, we get that $1+2+3+4+5+6=21>16$ . Then it's not possible to add up 6 different integers from 1 to 10 to a sum of 16 and therefore have such table with sum of 21.

To meet the given requirements, the left column and the right column must have 6 different numbers that add up to 42, of which there are 3 possibilities: (2, 6, 7, 8, 9, 10), (3, 5, 7, 8, 9, 10), and (4, 5, 6, 8, 9, 10). Out of these 3 possibilities, there is only 1 way each to split the 6 numbers into 2 sets of 3 numbers that add up to 21 each: (2, 9, 10) and (6, 7, 8) for the first, (3, 8, 10) and (5, 7, 9) for the second, and (4, 8, 9) and (5, 6, 10) for the third.

Since all 10 numbers must add up to 55, and the top and bottom rows must add to 21 each, the two middle numbers of both columns must add to 55 - 21 - 21 = 13. Using different numbers from 1 through 10, there are only 4 ways to do this: 3 and 10, 4 and 9, 5 and 8, and 6 and 7.

However, the only column grouping with a 3 is (3, 8, 10) and (5, 7, 9), so 10 must be in the same column as 3, so 3 and 10 cannot be the two middle numbers in separate columns. The only column grouping with a 4 is (4, 8, 9) and (5, 6, 10), so 9 must be in the same column as 4, so 4 and 9 cannot be the two middle numbers in separate columns. The only groupings with a 6 is (2, 9, 10) and (6, 7, 8) or (4, 8, 9) and (5, 6, 10), so 7 is either in the same column as 6 or 7 is not in either column, so either way 6 and 7 cannot be the two middle numbers in separate columns. This leaves 5 and 8 as the only possible middle numbers of both columns using either (3, 8, 10) and (5, 7, 9), or (4, 8, 9) and (5, 6, 10).

If 5 and 8 are the middle numbers of both columns using (3, 8, 10) as one column and (5, 7, 9) as the other column, the remaining numbers are 1, 2, 4, and 6. In one of the rows, 10 must either be with 7 or 9. If 10 is with 9, the remaining two numbers must add up to 21 - 10 - 9 = 2, which is impossible to achieve using two of the remaining numbers of 1, 2, 4, and 6. If 10 is with 7, the remaining two numbers must add up to 21 - 10 - 7 = 4, which is also impossible to achieve using two of the remaining numbers of 1, 2, 4, and 6.

If 5 and 8 are the middle numbers of both columns using (4, 8, 9) as one column and (5, 6, 10) as the other column, the remaining numbers are 1, 2, 3, and 7. In one of the rows, 10 must either be with 4 or 9. If 10 is with 9, the remaining two numbers must add up to 21 - 10 - 9 = 2, which is impossible to achieve using two of the remaining numbers of 1, 2, 3, and 7. If 10 is with 4, the remaining two numbers must add up to 21 - 10 - 4 = 7, which is also impossible to achieve using two of the remaining numbers of 1, 2, 3, and 7.

Therefore, 5 and 8 cannot be the two middle numbers in separate columns, and as shown earlier neither can any other possible sum of 13. Therefore, it is not possible to meet the given requirements for a sum of 21.