Magic With Maths
1 2 − 2 2 + 3 2 − 4 2 + . . . . . . + 9 9 2 − 1 0 0 2 = ?
The answer is -5050.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Good approach of recognizing the difference of two squares.
Note a^2-b^2=(a-b)(a+b) the latter is difference of sqaurs
Solution https://www.youtube.com/watch?v=MJSPTF14OY4&ab_channel=RazingThunderRazingThunder
It is easy to observe that if two terms are taken together, and a²-b²=(a+b)(a-b) is applied, the series can be collapsed to an easy arithmetic progression -3,-7,-11,….,199 with 50 terms.
Sum of this AP=50/2 [2(-3) + 49(-4)]=-5050. :)
Your solution is more difficult... Try this method...! :)
1 2 − 2 2 + 3 2 − 4 2 + . . . . . . + 9 9 2 − 1 0 0 2
The above is equal to ( 1 − 2 ) ( 1 + 2 ) + ( 3 − 4 ) ( 3 + 4 ) + . . . . . + ( 9 9 − 1 0 0 ) ( 9 9 + 1 0 0 )
That is equal to
( − 1 ) ( 1 + 2 ) + ( − 1 ) ( 3 + 4 ) + ( − 1 ) ( 5 + 6 ) + . . . . . . . + ( − 1 ) ( 9 9 + 1 0 0 )
Take − 1 outside..., then you will get it as − 1 × ( 1 + 2 + 3 + 4 + . . . . . . . . + 9 9 + 1 0 0 )
Simply using 2 n ( n + 1 ) , 1 + 2 + 3 . . . + 9 9 + 1 0 0 = 5 0 5 0
Then the answer will be − 1 × 5 0 5 0 = − 5 0 5 0
Simple...! :)
Log in to reply
Ya, for a person not familiar with sum of terms in an arithmetic progression, your method is better.
But most of the people attempting this problem would be familiar with the same, it doesn't make any difference.
But still, thanks for the advice. I take it in good stead. :)
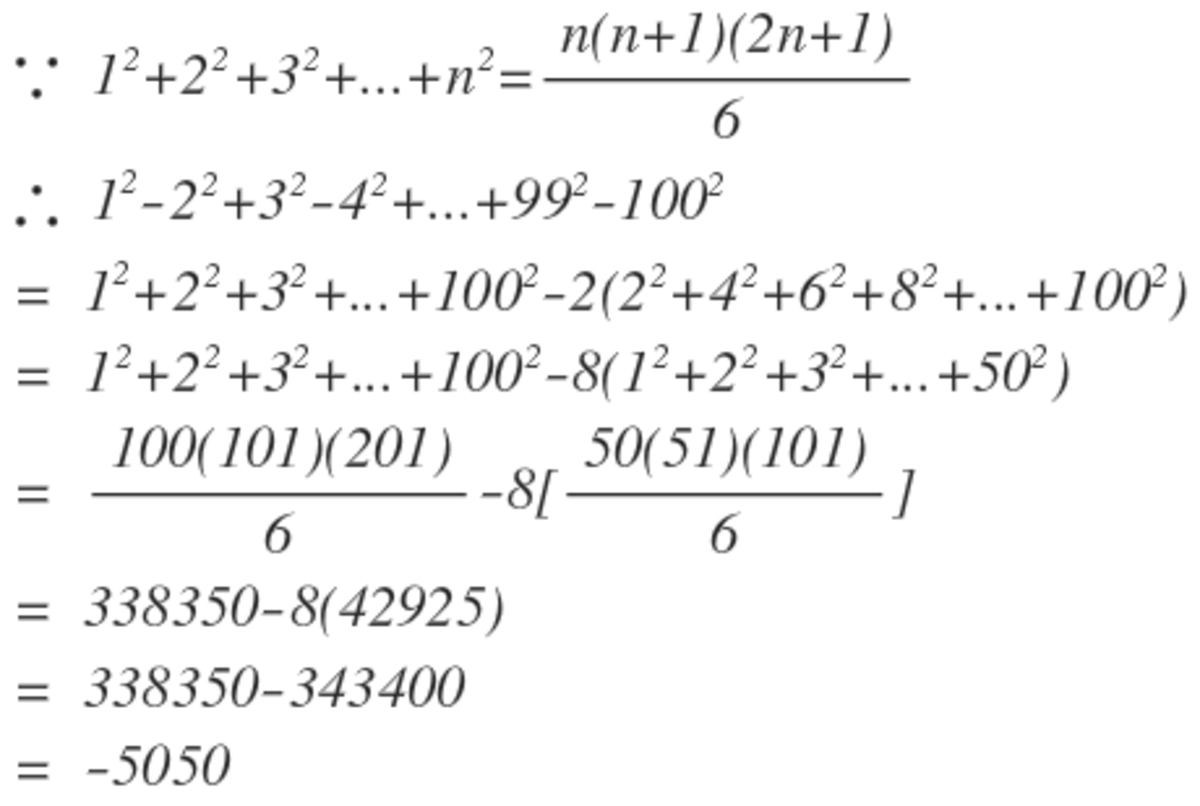
We can use telescoping. By observing the first few elements of the series, we observe a pattern -
{ 1 }^{ 2 }-{ 2 }^{ 2 }=\left( 1-2 \right) \left( 1+2 \right) =-1-2\\ { 3 }^{ 2 }-{ 4 }^{ 2 }=\left( 3-4 \right) \left( 3+4 \right) =-3-4
Let's see if the pattern is consistent by proving it.
= n 2 − ( n + 1 ) 2 = ( n + n + 1 ) ( n − n − 1 ) = − 1 ( 2 n + 1 ) = − 2 n − 1 = − n + ( − n − 1 )
Aha! Now we can use the pattern to simplify the series and write it as a AP.
= 1 2 − 2 2 + 3 2 − 4 2 + ⋯ + 9 9 2 − 1 0 0 2 = − 1 − 2 − 3 − 4 − ⋯ − 9 9 − 1 0 0 = − ( 1 + 2 + 3 + 4 + ⋯ + 9 9 + 1 0 0 )
Now we can simplify it using the summation formula .
= − ( 1 + 2 + 3 + 4 + ⋯ + 9 9 + 1 0 0 ) = − ( 2 1 0 0 ⋅ 1 0 1 ) = − 5 0 5 0