Magic_triangle
How many magic triangles are there for the chosen values of S and A 7 ?
{ A 1 , A 2 , A 3 , . . , A 1 5 , A 1 6 } - is permutation of set { 1 , 2 , 3 , . . , 1 5 , 1 6 }
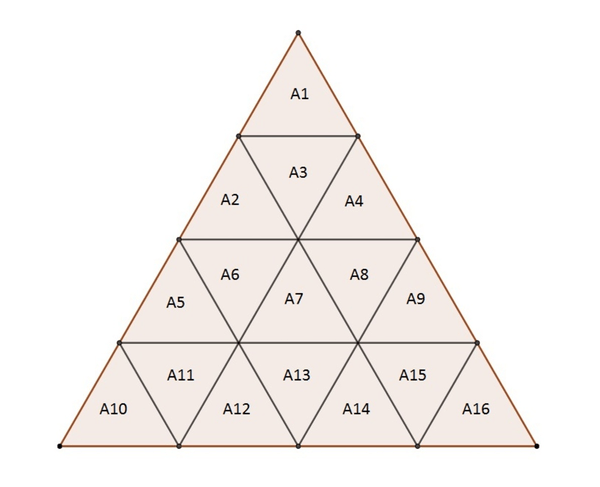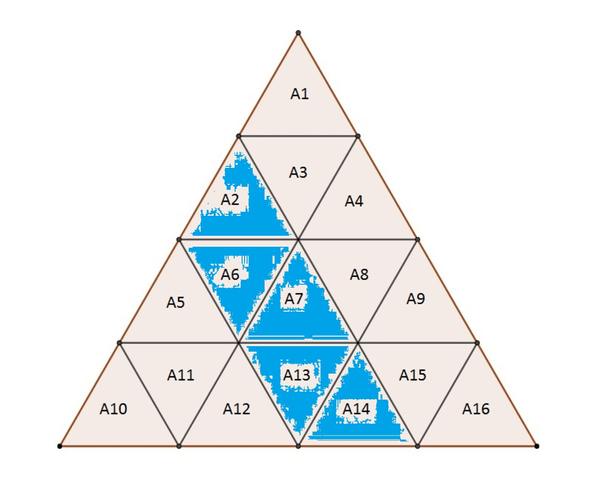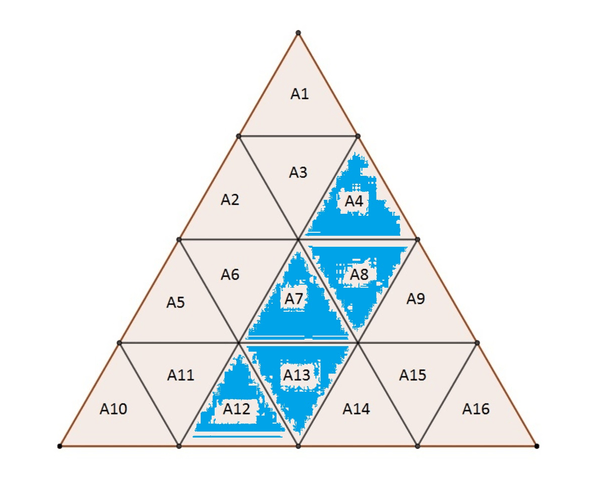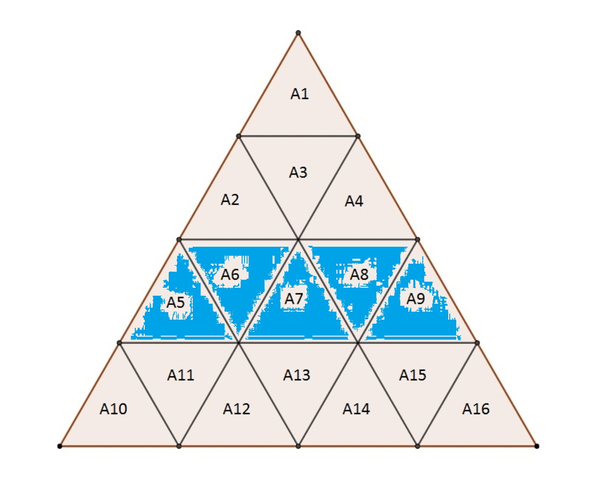
A 1 + A 2 + A 3 + A 5 + A 6 + A 1 1 + A 1 0 = S
A 1 + A 4 + A 3 + A 8 + A 9 + A 1 5 + A 1 6 = S
A 1 0 + A 1 1 + A 1 2 + A 1 3 + A 1 4 + A 1 5 + A 1 6 = S
A 5 + A 6 + A 7 + A 8 + A 9 = S
A 2 + A 6 + A 7 + A 1 3 + A 1 4 = S
A 4 + A 8 + A 7 + A 1 2 + A 1 3 = S
Let N ( S , A 7 ) be the number of magic triangles for the chosen values of S and A 7 . Find S m a x and A 7 m a x which give the maximum value of N ( S , A 7 ) . Give answer S m a x + A 7 m a x
The problem was proposed thanks to V. Ilyukhin.
The answer is 69.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The full dataset (where N ( S , A 7 ) = 0 ) is:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
|
Since A 1 , A 2 , A 3 , . . . , A 1 5 , A 1 6 is a permutation of the set 1 , 2 , 3 , . . . , 1 5 , 1 6 , that means n = 1 ∑ 1 6 A n = 1 + 2 + 3 + . . . + 1 5 + 1 6 = 2 1 ⋅ 1 6 ⋅ 1 7 = 1 3 6 .
Adding all six of the given equations and simplifying gives A 6 + A 7 + A 8 + A 1 3 = 6 S − 2 7 2 .
From third given equation A 1 0 + A 1 1 + A 1 2 + A 1 3 + A 1 4 + A 1 5 + A 1 6 = S and the fourth given equation A 5 + A 6 + A 7 + A 8 + A 9 = S , as well as n = 1 ∑ 1 6 A n = 1 3 6 , we obtain A 1 + A 2 + A 3 + A 4 = 1 3 6 − 2 S .
Similarly, A 5 + A 1 0 + A 1 1 + A 1 2 = 1 3 6 − 2 S and A 9 + A 1 4 + A 1 5 + A 1 6 = 1 3 6 − 2 S .
Let B = A 2 + A 4 + A 5 + A 9 + A 1 2 + A 1 4 , C = A 1 + A 3 + A 1 0 + A 1 1 + A 1 5 + A 1 6 , and D = A 6 + A 8 + A 1 3 .
From A 6 + A 7 + A 8 + A 1 3 = 6 S − 2 7 2 we get D + A 7 = 6 S − 2 7 2 .
From A 1 + A 2 + A 3 + A 4 = 1 3 6 − 2 S , A 5 + A 1 0 + A 1 1 + A 1 2 = 1 3 6 − 2 S , and A 9 + A 1 4 + A 1 5 + A 1 6 = 1 3 6 − 2 S we get B + C = 4 0 8 − 6 S .
From A 1 + A 2 + A 3 + A 5 + A 6 + A 1 0 + A 1 1 = S , A 1 + A 3 + A 4 + A 8 + A 9 + A 1 5 + A 1 6 = S , and A 1 0 + A 1 1 + A 1 2 + A 1 3 + A 1 4 + A 1 5 + A 1 6 = S we get B + 2 C + D = 3 S .
From A 2 + A 6 + A 7 + A 1 3 + A 1 4 = S , A 4 + A 7 + A 8 + A 1 2 + A 1 3 = S , and A 5 + A 6 + A 7 + A 8 + A 9 = S we get B + 2 D + 3 A 7 = 3 S .
Combining D + A 7 = 6 S − 2 7 2 , B + C = 4 0 8 − 6 S , B + 2 C + D = 3 S , and B + 2 D + 3 A 7 = 3 S we get B = − A 7 − 9 S + 5 4 4 , C = A 7 + 3 S − 1 3 6 , and D = − A 7 + 6 S − 2 7 2 .
For S ≤ 4 9 and 1 ≤ A 7 ≤ 1 6 , B ≥ 8 7 . However, the highest value that B can be is 1 1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 = 8 1 . Therefore, S ≥ 5 0 .
For S ≥ 5 6 and 1 ≤ A 7 ≤ 1 6 , D ≥ 4 8 . However, the highest value that D can be is 1 4 + 1 5 + 1 6 = 4 5 . Therefore, S ≤ 5 5 .
Armed with 5 0 ≤ S ≤ 5 5 and the above equations, we can now use a computer program to brute force each possible number of magic triangles for chosen values of S and A 7 . (Note: this still took over 16 hours on my computer to run!)
Ignoring symmetrical and rotational equal possibilities, the S and A 7 values that give the maximum number of magic triangles is S max = 5 3 and A 7 max = 1 6 at 3 0 8 8 possible triangles. Therefore, S max + A 7 max = 5 3 + 1 6 = 6 9 .