Magnetic Field from Current Doughnut

Electricity and Magnetism Level 3

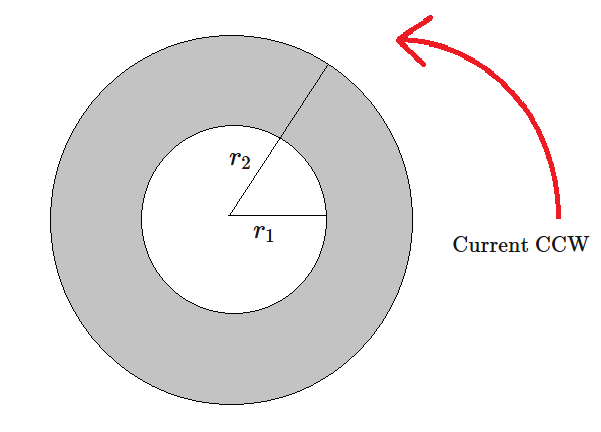
A thin, flat "doughnut"-shaped piece of metal with inner radius r 1 r_1 and outer radius r 2 r_2 carries a total current I I which circulates in the counter-clockwise direction. The current is uniformly distributed over the doughnut's area.

What is the magnitude of the magnetic flux density at the center of the doughnut (in micro-Teslas ( μ T ) (\mu T) )?

Details and Assumptions:

  • r 1 = 1 m r_1 = 1 \, \text{m}
  • r 2 = 2 m r_2 = 2 \, \text{m}
  • I = 100 A I = 100 \, \text{A}
  • μ 0 = 4 π × 1 0 − 7 H/m \mu_0 = 4 \pi \times 10^{-7} \, \text{H/m}

Bonus: How does this compare to the strength of the Earth's magnetic field at the Earth's surface?


The answer is 41.888.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Steven Chase
Feb 24, 2018

Represent the doughnut as a combination of current loops. In general, the B-field at the center of a single current-carrying loop is:

B = μ 0 I 2 R \large{B = \frac{\mu_0 \, I}{2 \, R}}

Total area:

A = π ( r 2 2 − r 1 2 ) \large{A = \pi \, (r_2^2 - r_1^2)}

Infinitesimal ring area:

d A = 2 π r d r \large{dA = 2 \pi r \,dr}

Infinitesimal ring current (assuming total current is I I ):

d I = I 2 π r d r π ( r 2 2 − r 1 2 ) = 2 I r 2 2 − r 1 2 r d r \large{dI = I \frac{2 \pi r \,dr}{\pi \, (r_2^2 - r_1^2)} = \frac{2 I}{r_2^2 - r_1^2} \, r \, dr}

Magnetic flux density contribution at center:

d B = μ 0 d I 2 r = μ 0 2 r 2 I r 2 2 − r 1 2 r d r d B = μ 0 I r 2 2 − r 1 2 d r \large{dB = \frac{\mu_0 \, dI}{2 \, r} = \frac{\mu_0}{2 \, r} \frac{2 I}{r_2^2 - r_1^2} \, r \, dr \\ dB = \frac{\mu_0 \, I}{r_2^2 - r_1^2} \, dr}

Total magnetic flux density:

B = μ 0 I r 2 2 − r 1 2 ∫ r 1 r 2 d r = μ 0 I ( r 2 − r 1 ) r 2 2 − r 1 2 ≈ 41.888 μ T \large{B = \frac{\mu_0 \, I}{r_2^2 - r_1^2} \int_{r_1}^{r_2} dr = \frac{\mu_0 \, I \, (r_2 - r_1)}{r_2^2 - r_1^2} \approx 41.888 \, \mu T}

1 Helpful 1 Interesting 1 Brilliant 0 Confused

@Steven Chase Hello Telegram is a app.
You can install it using playstore .
We can contact each other with that without the use of phone number .
My Telegram id is “Chase4712”.


Talulah Riley - 4 days, 19 hours ago

@Steven Chase why don't you want to use Telegram app.
After 2 July ,2021 where will you upload your problems ??
How Brilliant will get benefit by this blunder ?
Will you keep donating to Brilliant for premium membership after 2 July ??
I will make a website which is only for uploading good problems and solutions.
Please reply.
Thanks in advance.

Talulah Riley - 4 days, 10 hours ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...