Magnetic Field from Current Strip
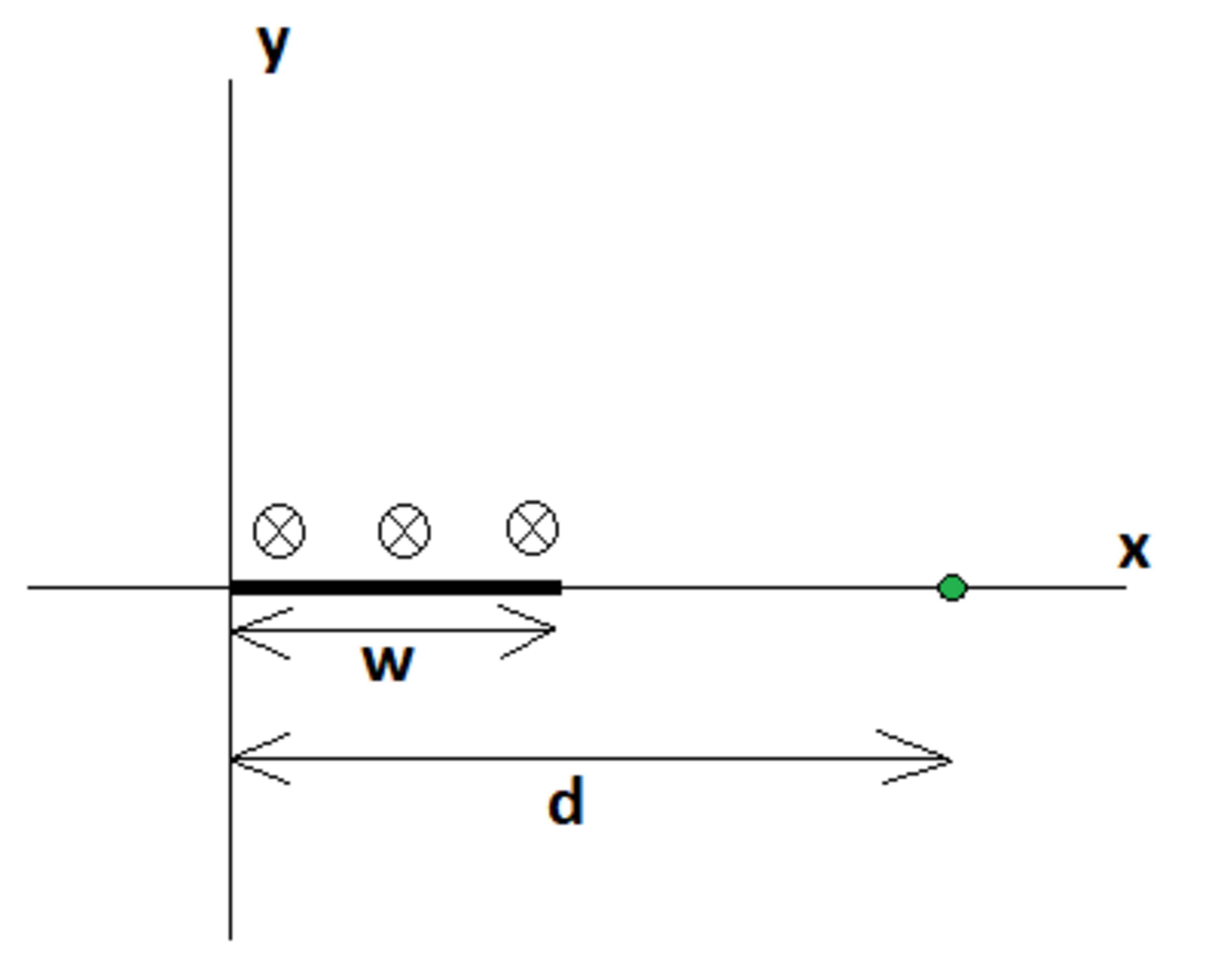
In the plane, a thin metal strip of width is oriented with its left side at and its right side at . The strip has infinite length, and its length is perpendicular to the plane.
The strip carries a constant current of , uniformly distributed over its width. The current is directed into the page.
There is a test point on the -axis at a distance from the origin.
What is the magnitude of the magnetic flux density at the test point?
Details and assumptions:
- The surrounding medium is vacuum.
- Give your answer in nano-Teslas, to 3 decimal places.
The answer is 138.629.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let l = x i ^ + z k ^ be the parametrization of the metal strip, where z goes from − ∞ to ∞ and x goes from 0 to 1 . Let's find the magnetic field in a point P = d i ^ . By Biot-Savart Law we have: B = 4 π μ 0 I ∫ 0 1 ∫ − ∞ ∞ ∥ ∥ ∥ P − l ∥ ∥ ∥ 3 d l × ( P − l ) d x = 4 π μ 0 I ∫ 0 1 ∫ − ∞ ∞ ∥ ∥ ∥ ( d − x ) i ^ − z k ^ ∥ ∥ ∥ 3 ( d − x ) j ^ d z d x = 4 π μ 0 I ∫ 0 1 ∫ − ∞ ∞ ( ( d − x ) 2 + z 2 ) 3 / 2 ( d − x ) j ^ d z d x = 4 π μ 0 I ∫ 0 1 d − x 1 ∫ − π / 2 π / 2 cos θ j ^ d θ d x = 2 π μ 0 I ∫ 0 1 d − x 1 d x = 2 π μ 0 I ( ln ( d ) − ln ( d − 1 ) ) Finally, substituting d = 2 m and I = − 1 A we have B = − 2 × 1 0 − 7 ln ( 2 ) j ^ T , and ∥ ∥ ∥ B ∥ ∥ ∥ ≈ 1 3 8 . 6 2 9 nT .