Magnetic Field From Square Wire
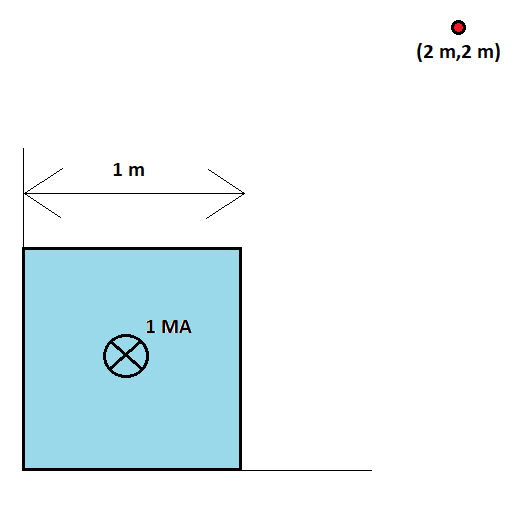
A huge superconducting wire with a square cross-section carries a constant DC current of one million ( ) amps. The wire is infinitely long, and its cross-section has a side length of .
What is the magnitude of the magnetic flux density ( ) at the point (in milli-Teslas)?
Details and Assumptions:
- Use the free-space permeability constant.
- The wire's lower left corner is at the origin in the plane, and its length is along the -axis (into the page).
- The current flow is along the -axis (into the page), and the current density is uniform over the cross-section.
- The sides of the square cross-section are aligned with the and axes.
Bonus: The assumption of uniform current density, while convenient, is dubious in light of actual superconductor physics. See the Meissner Effect for a primer on superconductor fundamentals. Thanks to Laszlo Mihaly for pointing this out.
The answer is 94.37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider a very thin infinite long wire carries a current I placed along z-axis (into the page). The magnetic field at r 0 = ( x 0 , y 0 ) is given by B = 2 π r 0 2 μ 0 I ( − k ^ × r 0 ) .
Now, let consider the small partition of the wire with area d A = d x d y placed at r = ( x , y ) . Since the current density is uniform along the cross section, then the partition carries current d I = A I d A = I d x d y . Using the result above, the magnetic field of the partition at r 0 = ( x 0 , y 0 ) is given by d B = = 2 π ∣ r 0 − r ∣ 2 μ 0 d I [ − k ^ × ( r 0 − r ) ] 2 π μ 0 I ( y 0 − y ) 2 + ( x 0 − x ) 2 ( y 0 − y ) i − ( x 0 − x ) j d x d y .
With x 0 = 2 m and y 0 = 2 m , the x-component of magnetic field, B x = 2 π μ 0 I ∫ 0 1 ∫ 0 1 ( y 0 − y ) 2 + ( x 0 − x ) 2 ( y 0 − y ) d x d y = 6 6 . 8 m T , and the y-component of magnetic field B y = − 2 π μ 0 I ∫ 0 1 ∫ 0 1 ( y 0 − y ) 2 + ( x 0 − x ) 2 ( x 0 − x ) d x d y = − 6 6 . 8 m T .
Thus, the magnitude of magnetic field at r 0 = ( x 0 , y 0 ) = ( 2 , 2 ) m is B = B x 2 + B y 2 = 9 4 . 3 7 m T .