Magnetic field of a rotating sphere
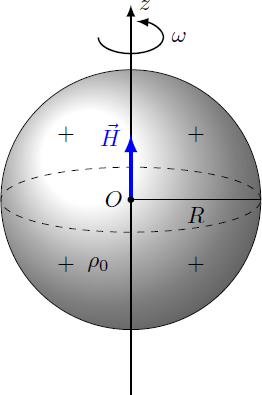
A sphere with the radius is homogeneously charged with the charge distribution where is the total charge. The sphere rotates at the frequency around its own axis.
What is the absolute value of the magnetic field caused by the rotation in the center of the sphere?
Specifies the result in units of ampere per meter.
The answer is 500.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The charges move on circles aroud the z axis with the velocity v = 2 π f r ⊥ e φ , where r ⊥ = r sin θ denotes the distance from the ration axis. The currents density yields j = ρ v = ρ ω r sin θ e ϕ with the charge desinty ρ = 3 4 π R 3 Q of the sphere. The magnetic field at the point r 0 results according to the Biot-Savart law: H ( r 0 ) = 4 π 1 ∫ ∣ r 0 − r ∣ 3 j ( r ) × ( r 0 − r ) d V First, we calculate the cross product j ( r ) × ( r 0 − r ) = − ρ ω r sin θ ⎝ ⎛ − sin ϕ cos ϕ 0 ⎠ ⎞ × ⎝ ⎛ r cos ϕ sin θ r sin ϕ sin θ r cos θ ⎠ ⎞ = − ρ ω r 2 sin θ ⎝ ⎛ cos ϕ cos θ sin ϕ cos θ − sin θ ⎠ ⎞ Now we can calculate the magnetic field by volume integration in spherical coordinates: H ( 0 ) = − 4 π 1 ∫ 0 2 π ∫ 0 π ∫ 0 R r 3 ρ ω r 2 sin θ ⎝ ⎛ cos ϕ cos θ sin ϕ cos θ − sin θ ⎠ ⎞ r 2 sin θ d r d θ d ϕ = − 4 π ρ ω ∫ 0 π ∫ 0 R r sin 2 θ ⎝ ⎛ 0 0 − 2 π sin θ ⎠ ⎞ d r d θ = 2 ρ ω ∫ 0 R r d r ∫ 0 π sin 3 θ d θ e z = 3 8 π R 3 Q ω ⋅ 2 R 2 ⋅ 3 4 e z = 2 R Q f e z The absolute value of the magnetic field thus results ∣ H ∣ = 2 R Q f = 2 ⋅ 0 . 1 1 ⋅ 1 0 0 m A = 5 0 0 m A