Magnetic Fields from Two Elliptical Wires
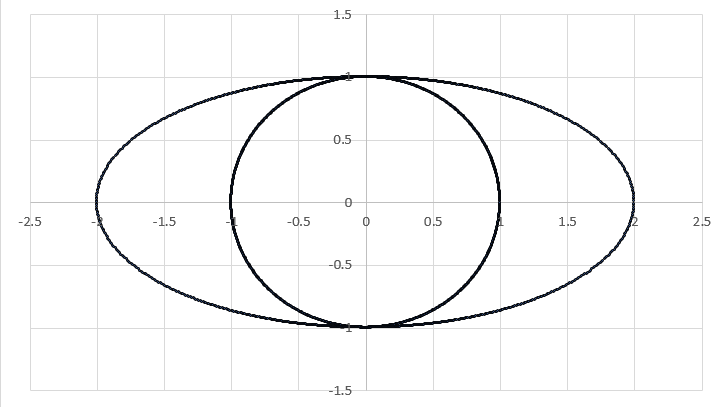
Consider two elliptical wires (one of which happens to be a circle):
If we pass 1 amp of current through the circular wire, the magnitude of the magnetic field at the origin is . If we pass 1 amp of current through the elliptical wire, the magnitude of the magnetic field at the origin is .
What is ?
Note: The wires are not connected, even though they are both shown on the same graph. The wire cross section is much smaller than the ellipse axial lengths, and the currents circulate around the origin.
The answer is 0.77098.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This boils down to an application of the Biot-Savart Law for current-carrying loops:
B = 4 π μ 0 I ⋅ ∮ R 1 d θ (i)
For the circular loop, we compute B C as:
B C = 4 π μ 0 I ⋅ ∫ 0 2 π R 1 d θ = 4 π R μ 0 I θ ∣ 0 2 π = 2 R μ 0 I (ii)
and substituting R = 1 and I = 1 gives B C = 0 . 5 μ 0
For the elliptical loop (with coordinates ( x , y ) = ( 2 c o s ( θ ) , s i n ( θ ) ) ) , the radius is now equal to R = a 2 s i n 2 ( θ ) + b 2 c o s 2 ( θ ) a b = 2 2 s i n 2 ( θ ) + 1 2 c o s 2 ( θ ) ( 2 ) ( 1 ) = 3 s i n 2 ( θ ) + 1 2 . Substituting this expression into (i) now produces:
B E = 4 π μ 0 I ⋅ 4 ∫ 0 2 π R 1 d θ = π μ 0 I ⋅ ∫ 0 2 π 2 3 s i n 2 ( θ ) + 1 d θ (iii)
which the integrand is a complete elliptical integral of the second-kind (with parameter k 2 = 3 ). The final computation for (iii) (which I'll use Wolfram Alpha on the elliptical integral) yields:
B E = 2 π μ 0 I ⋅ ∫ 0 2 π 3 s i n 2 ( θ ) + 1 d θ = 2 π μ 0 ( 1 ) ⋅ 2 . 4 2 2 1 1 ⇒ B E = 0 . 3 8 5 7 μ 0 .
Thus, the we arrive at the desired ratio of magnetic fields at the origin: B C B E = 0 . 5 μ 0 0 . 3 8 5 7 μ 0 = 0 . 7 7 1 .