Magnetic Flux (5-25-2021)
Consider the following closed curve in the x y plane (curve x y coordinates are in meters).
r ( θ ) x ( θ ) y ( θ ) z 0 ≤ = = = = θ 1 + 2 1 sin ( 4 θ ) r ( θ ) cos θ r ( θ ) sin θ 0 ≤ 2 π
There is a magnetic flux density B throughout all of space. The field is perpendicular to the x y plane.
B = ( B x , B y , B z ) = ( 0 , 0 , 3 x 2 ) m 2 Wb
Determine the absolute value of the magnetic flux (in Wb ) through the interior surface bounded by the curve.
∬ S B ⋅ d S
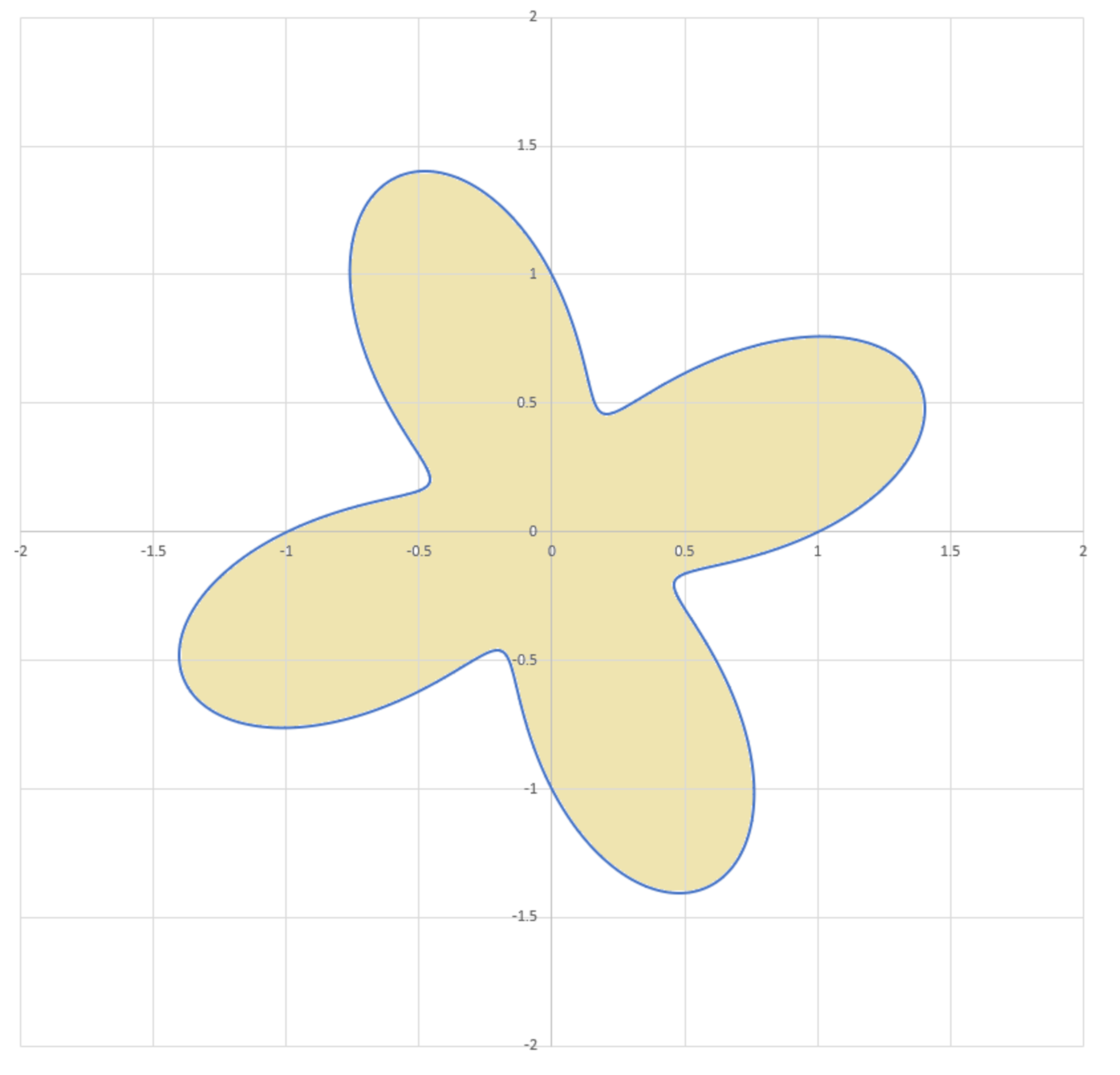
The answer is 4.1785.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
In hindsight, this problem could have been solved without invoking the concept of the vector potential. I have added a much shorter solution at the end of my already posted solution.
Greetings! I could use a helpful hint to compute the curve of intersection in your latest problem. I am struggling to solve it.
First, the magnetic vector potential is computed using the relation:
∇ × A = B ∂ y ∂ A z − ∂ z ∂ A y = 0 ∂ z ∂ A x − ∂ x ∂ A z = 0 ∂ x ∂ A y − ∂ y ∂ A x = 3 x 2
From the above relations, with a little bit of trial and error, it is seen that the following vector satisfies the above relations.
A = 0 i ^ + x 3 j ^ + 0 k ^
Now, by applying Stokes' theorem
Φ = ∫ ∫ S B ⋅ d S = ∫ ∫ S ( ∇ × A ) ⋅ d S = ∮ C A ⋅ d R
R = r ( θ ) cos θ i ^ + r ( θ ) sin θ j ^ d θ d R = d θ d ( r ( θ ) cos θ ) i ^ + d θ d ( r ( θ ) sin θ ) j ^
Plugging in the given parameterization:
⟹ Φ = ∮ C A ⋅ d R = ∫ 0 2 π ( x 3 ( θ ) d θ d ( r ( θ ) sin θ ) ) d θ
Simplifying the integrand leads to:
Φ = ∮ C A ⋅ d R = ∫ 0 2 π ( 1 + 0 . 5 sin 4 θ ) 3 cos 3 θ ( 2 sin θ cos 4 θ + cos θ ( 1 + 0 . 5 sin 4 θ ) ) d θ
Φ = 5 1 2 6 8 1 π ≈ 4 . 1 7 8 5 6 3 6 6 6 2 0 0 4 8 7
Shorter method:
B = 3 r 2 cos 2 θ k ^ d S = r d r d θ k ^
Φ = ∫ ∫ S B ⋅ d S = ∫ 0 2 π ∫ 0 1 + 0 . 5 sin 4 θ ( 3 r 2 cos 2 θ ) r d r d θ ≈ 4 . 1 7 8 5 6 3 6 6 6 2 0 0 4 8 7