Magnetic flux + Calculus = MagaCulus
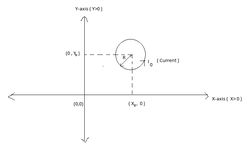 Let an circular current loop is placed in X-Y co-ordinate plane such That it's centre
lies on Point
P
(
x
0
,
y
0
)
in First quadrant.
Let an circular current loop is placed in X-Y co-ordinate plane such That it's centre
lies on Point
P
(
x
0
,
y
0
)
in First quadrant.
Let I 0 current is flowing in the Loop. Then find The Magnetic flux passing through The X-Y plane where X - Coordinate Has The restriction That:
X ≤ 0
Details
- R = 1 m
- x 0 = 2 m
- y 0 = 4 m
- I 0 = 8 × 1 0 7 C/s
This is part of set Mixing of concept
The answer is 26.93.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This was a really brilliant problem Deepanshu!! Just loved solving it!! ⌣ ¨
Nice question ! Learnt new thing
jst gr8 i took it as a dipole [ acc to a theory ] and then integrated ans was coming out to be 25.3 probably it was wrong because the dipole is not short :(
Nice solution.
Bro you are genius
Yep Mutual induction makes this a classic Nice problem
Consider the boundary of the region X ≤ 0 as a rectangular loop. Let ϕ be the required flux.
ϕ = M I 0 , where M is the coefficient of mutual induction.
If we introduce current I in the rectangular loop. Let ϕ ′ be the flux in the loop due to this current.
Clearly,
ϕ ′ = M I
Clearly, ϕ ′ is due to Y − a x i s only, because other wires are far away from the loop contributing to negligiblle magnetic flux.

Clearly,
ϕ ′ = ∫ 1 3 2 π r μ 0 I 2 1 − ( 2 − r ) 2 d r
= ( 8 − 4 3 ) π I (Using the substitution ( 2 − r ) = sin θ )
Clearly, M = ( 8 − 4 3 ) π Henry
Hence, ϕ = M I 0 = 2 6 . 9 4 Tm 2
Hey @jatin yadav You Check your calculation according to this your answer would be 13.468 .
And Sorry Since just after your solution I upload my because while you upload your's at the same time I'am uploading mine..!! I didn't Know about This..!! Mine Solution is Lengthy So It takes more Time ..So sorry Once again
Log in to reply
Yes, thanks for pointing that out. Actually, II missed to show a 2 in the solution. And no problem :)
@jatin yadav can you add more steps on how to evaluated the integral.thanks
To find the magnetic flux passing through the X-Y plane when X<0 it is difficult to direct integrate it..!! So let's Do some Different.
Assume an Hypothetical current carrying wire which is Placed on entire Y-axis and whose ends are connected at infinity so that they form a Square Type loop. Also Let the current flowing in the square Loop is I 1
Now name the two loop. Call circular loop to be 2 and the square loop as 1.
And Let Mutual inductance between these Loops is " M "
ϕ 2 = M I 1 ⟶ ( 1 ) .
Also
ϕ 2 = ∫ B 1 d A 2 cos π .
now Consider an rectangular strip in the circular loop-2 of width dx which is at an distance of x From the loop-1 (From y-axis)
So According to figure :
x = x 0 − R sin θ d x = − R cos θ d θ B 1 = 2 π x μ 0 I 1 d A 2 = l d x = − ( 2 R cos θ ) R cos θ .
So magnetic flux passing through Loop-2 is
ϕ 2 = π μ 0 I 1 R 2 ∫ π / 2 − π / 2 x 0 − R sin θ cos 2 θ d θ ϕ 2 = π μ 0 I 1 R 2 ( ( 2 − 3 ) π ) ⟶ ( 2 ) .
Now comparing equation 1 and 2 we get value of M that is :
M = π μ 0 R 2 ( ( 2 − 3 ) π ) .
Now The Magnetic Flux Passing through The X-Y Plane where (X < 0 ) is equal to magnetic flux passing through the Loop-1
ϕ ( X Y − P l a n e X ≤ 0 ) = ϕ 1 = M I l o o p − 2 = π μ 0 R 2 I 0 ( ( 2 − 3 ) π ) = 2 6 . 9 3 A n s .