Magnetic Force - Different Segment Shapes

Electricity and Magnetism Level 4

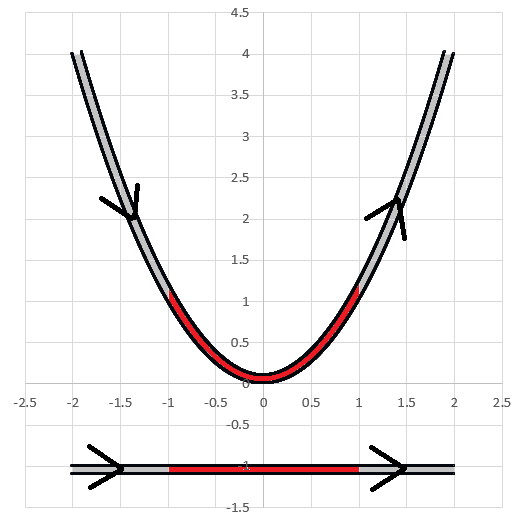
Infinitely long thin wires in the shape of the curves $y = x^2$ and $y = -1$ both carry constant currents of $1000$ amps. Segments 1 and 2 are the portions of both wires (shown in red) between $x = -1$ and $x = 1$ .

What is the magnitude of the magnetic force exerted by Segment 1 on Segment 2?

Details and Assumptions:
- Everything in standard SI units
- $\mu_0 = 4 \pi \times 10^{-7} \, \text{H/m}$

The answer is 0.1825.

2 solutions

Karan Chatrath
Mar 20, 2019

I had a go at the problem much later than when it was posted, but anyway, here's what I did:

I must point out that there is a bit of ambiguity in the problem statement. Segment 1 and 2 are not clearly labelled, and this was a cause for some initial confusion. Also, there might be some notation inconsistency in the solution but I have tried to be clear and concise. Feedback on the solution, as always, will be appreciated.

Thanks for the solution. I had forgotten that nobody had solved this one. I have others like that as well. I figured that due to Newton's Third Law, it didn't matter which was Segment 1 and which was Segment 2.

Steven Chase - 2 years, 2 months ago

@Steven Chase this question is very beautiful. Please post more question like this. I am waiting.

A Former Brilliant Member - 1 year, 7 months ago

Thanks. I’ll see if I can post another one this week

Steven Chase - 1 year, 7 months ago

There is a new one up now in the E and M section

Steven Chase - 1 year, 7 months ago

Thank you for the problem.

On a different note, I have recently posted my first problem on Brilliant. Please take a look and share your thoughts when possible.

https://brilliant.org/problems/golfer-meets-physicist/

Karan Chatrath - 2 years, 2 months ago

It looks very nice. I'll do it this evening.

Steven Chase - 2 years, 2 months ago

Steven Chase
Nov 11, 2018

General solution outline:

1) For each point on Segment 1, integrate over the entire Segment 2 using the Biot-Savart Law to determine the B-field at the Segment 1 point due to Segment 2

2) Calculate the infinitesimal force at each point on Segment 1 using $\vec{dF} = I \, \vec{dL} \times \vec{B}$

3) Add up the infinitesimal forces on Segment 1 to get the total force

Please more detailed

Mema Magdy - 2 years, 5 months ago

There is a more detailed solution now

Steven Chase - 2 years, 2 months ago

@Steven Chase can you please post more question like this one?.This question is very beautiful.

A Former Brilliant Member - 1 year, 7 months ago

Magnetic Force - Different Segment Shapes

The answer is 0.1825.

2 solutions

0 pending reports