Magnetic force on a loop
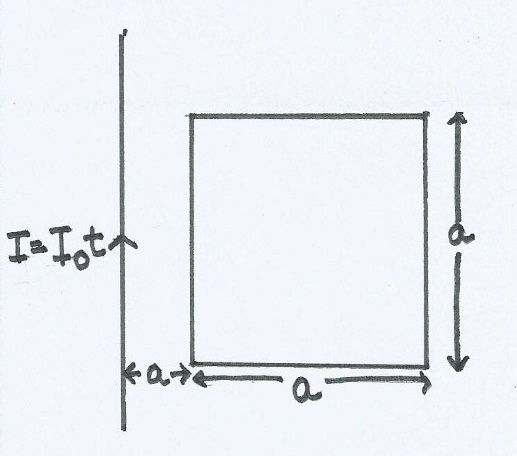
A long wire carrying current is fixed near a fixed conducting square coil of resistance as shown in the figure. The current in the long wire varies as . Find the net force acting on the coil at t = 2sec. Find the answer in SI units. [given and ln2 = 0.693 ]
The answer is 1.386.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider a vertical strip inside the loop of infinitesimal horizontal width d x and vertical length a which lies at a distance x from the infinitely long current carrying wire. The magnetic flux associated with this infinitesimal area will be
d Φ = B d S = 2 π x μ 0 I ⋅ a d x
Total magnetic flux through the loop would thus be
Φ B = ∫ a 2 a 2 π x μ 0 I ⋅ a d x = 2 π μ 0 I a ln ( 2 ) = 2 π μ 0 I 0 t a ln ( 2 )
Using Faraday's law's, the emf generated in the loop will be
E = ∣ ∣ ∣ ∣ d t d Φ B ∣ ∣ ∣ ∣ = 2 π μ 0 I 0 a ln ( 2 )
and the current associated with the loop will be
i = R E = 2 π R μ 0 I 0 a ln ( 2 )
F = i a ( 2 π a μ 0 I − 2 π ( 2 a ) μ 0 I ) = 2 π R μ 0 I 0 a ln ( 2 ) ( 2 π ( 2 ) μ 0 I 0 t ) = 1 . 3 8 6