Magnetic Force On this disk !!
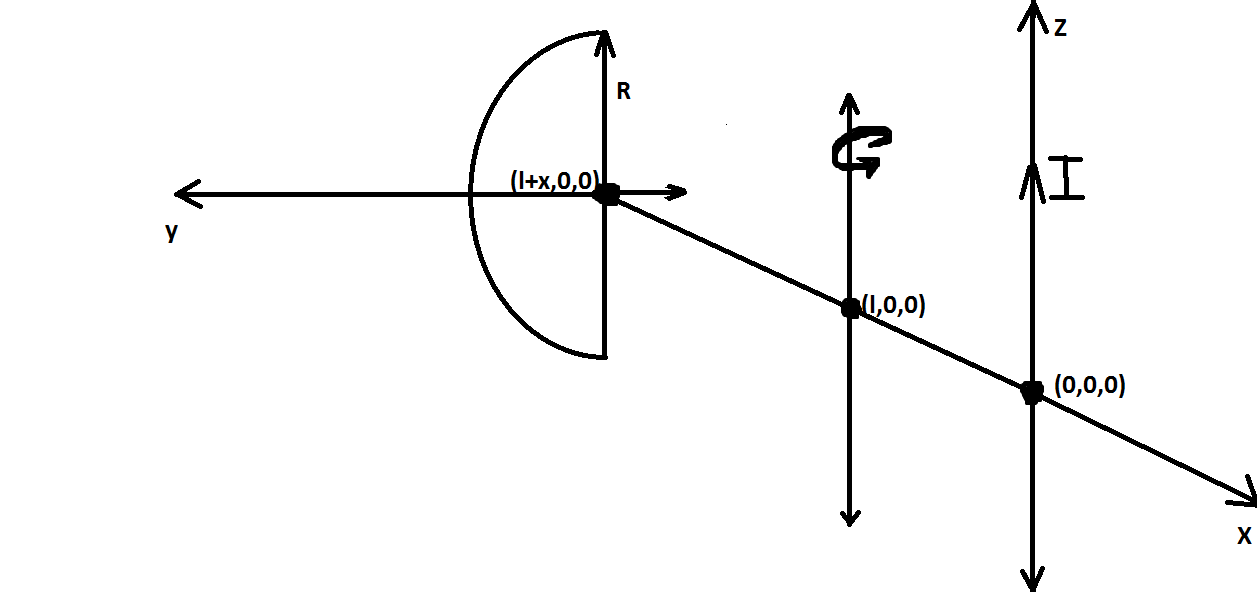 In the figure given above, the wire carries a current
I
.
The disk is made up of a non-conducting material with a charge density
.The disk is rigidly attached to the axis passing through the point
(L,0,0)
(along the z axis) with the help of a rigid rod of length
x
which is along the x axis.The axis is fixed.Now the disk is rotated about this axis with an angular velocity
(as shown in the figure) with the direction of the angular velocity vector coinciding with the current flow direction.The radius of this disk is
R
.The distance between the center of the disk and the axis is
x
(as shown in the figure). Find the magnetic force which acts on the disk just after it is given this angular velocity. (in Newtons)
Given:
R=1m;
L=5m;
x=1m;
I=10
A;
=2rad/s;
= 7C/m
In the figure given above, the wire carries a current
I
.
The disk is made up of a non-conducting material with a charge density
.The disk is rigidly attached to the axis passing through the point
(L,0,0)
(along the z axis) with the help of a rigid rod of length
x
which is along the x axis.The axis is fixed.Now the disk is rotated about this axis with an angular velocity
(as shown in the figure) with the direction of the angular velocity vector coinciding with the current flow direction.The radius of this disk is
R
.The distance between the center of the disk and the axis is
x
(as shown in the figure). Find the magnetic force which acts on the disk just after it is given this angular velocity. (in Newtons)
Given:
R=1m;
L=5m;
x=1m;
I=10
A;
=2rad/s;
= 7C/m
The answer is 2.564.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We go at a distance y from the center of the disc in the y-direction and take an elemental thin rod of width dy.Its length will be 2 R 2 − y 2 . Therefore its area is 2 R 2 − y 2 dy and the charge on it will be 2 R 2 − y 2 σ dy. Now the magnetic force acting on it will be dF=QvBsin α . Looking at the figure we can say that α = π \2 - θ - β .Thus sin α =cos( θ + β ).Solving this we get sin α = ( x 2 + y 2 ) ( ( L + x ) 2 + y 2 ) L y . Also, B= 2 π ( L + x ) 2 + y 2 μ 0 I and v= ω x 2 + y 2 .Putting these values in place of dF we finally get dF= π ( ( l + x ) 2 + y 2 ) I L μ 0 σ ω R 2 − y 2 y d y . Integrating this expression from y=0 to y=R we get π I L μ 0 σ ω ∫ y 2 + ( x + L ) 2 y R 2 − y 2 d y = π I L μ 0 σ ω [ 2 x 2 + 2 L x + R 2 + l 2 ln ( R 2 − y 2 + x 2 + 2 L x + R 2 + L 2 ∣ ∣ R 2 − y 2 − x 2 + 2 L x + R 2 + L 2 ∣ ∣ ) + R 2 − y 2 ] Note that the expression given above is the indefinite integral.We would have to put the limits from y=0 to y=+R and then, we would get the final answer.