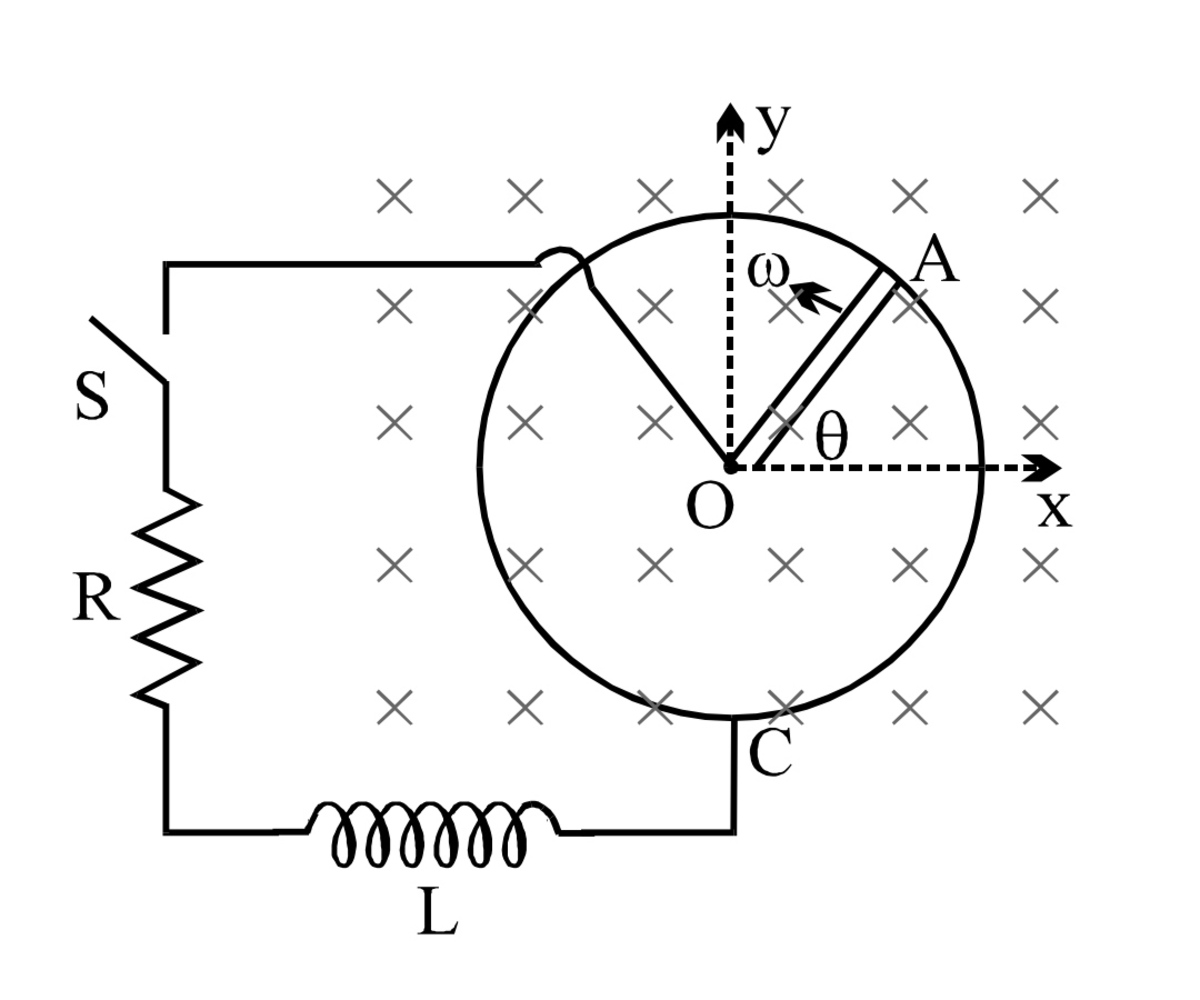
Magnetic Induction and Resistance

A metal rod OA of mass $m$ and length $r$ is kept rotating with a constant angular speed $\omega$ in a vertical plane
about a horizontal axis at the end O. The free end A is arranged to slide without friction along a fixed conducting circular ring in the same plane as that of rotation. A uniform and constant magnetic induction $\vec{B}$ is applied perpendicular and into the plane of rotation as shown in figure. An inductor $L$ and an external resistance $R$ are connected through a switch $S$ between the point $O$ and a point $C$ on the ring to form an electrical circuit. Neglect the resistance of the ring and the rod. Initially, the switch is open.

Obtain an expression for the current as a function of time after switch S is closed.
If your answer comes in the form of $I=\frac{B \omega r^{\alpha}(1-e^{(\frac{\beta Rt}{L})})}{\gamma R}$

Type your answer as $\alpha+\beta+\gamma$

Bonus:
Obtain the time dependence of the torque required to maintain the constant angular speed, given that the rod $OA$ was along the positive $X$ axis at $t=0$ .