Magnetic Moment of a loop
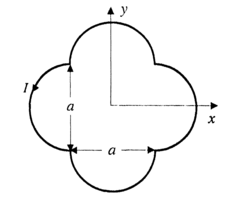 A loop carrying current
lies in the
plane as shown in the figure. The unit vector
is coming out of the plane of the paper. The magnetic moment of the current loop is
A loop carrying current
lies in the
plane as shown in the figure. The unit vector
is coming out of the plane of the paper. The magnetic moment of the current loop is
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We need the area enclosed in the loop, which is ( 2 π + 1 ) a 2 . Multiply this by the current I. Using the right-hang rule, we have the cross product pointing out of the page. Hence, the answer is
( 2 π + 1 ) ( a 2 ) I k ^ .