Magnetic permeability

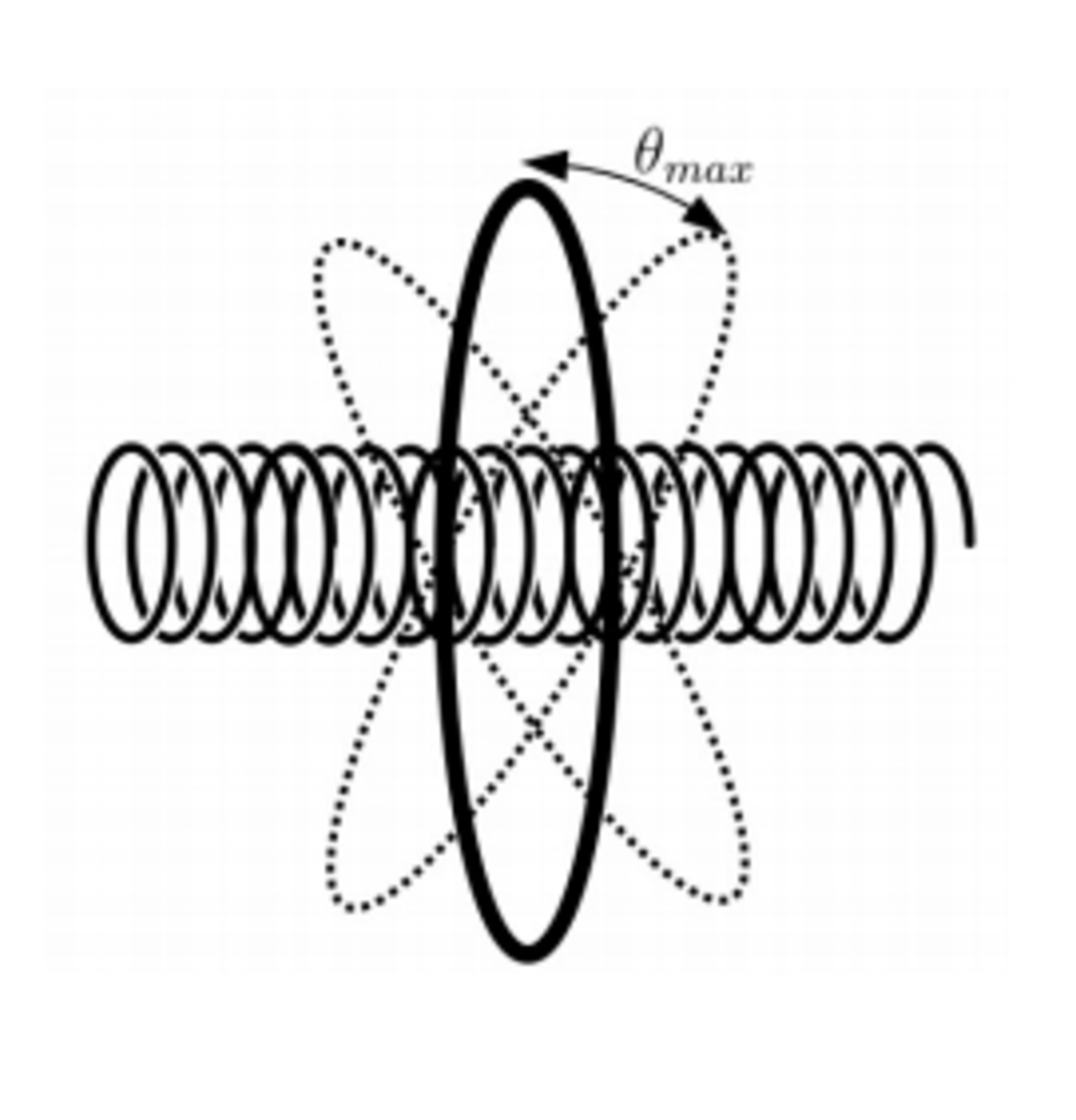
The figure shows a circular loop of radius a and resistance $R$ , centered on the axis of a very long solenoid, with $n$ turns per unit length and radius $b (b <a)$ . At the initial moment, $t = 0,$ the axis of the solenoid is perpendicular to the spiral plane, which oscillates according to the expression $\Theta = \Theta _{max}\sin (\omega t)$ , where $\omega$ is the angular frequency of motion. If the current passing through the solenoid grows linearly over time, as $I = Kt$ , and being $\mu _0$ the magnetic permeability of the vacuum, then the intensity of the induced electric current in the loop is

Can you help me?