Magnetic takeoff
A thin charged loop with a charge
q
>
0
(uniformly distributed) and mass
m
is placed on a ramp which forms and angle
α
=
4
5
∘
with the horizontal. Due to the presence of an external homogeneous magnetic field of magnitude
B
directed into the page, the loop "takes off" after a time
t
∗
. Determine the time
t
∗
in seconds
if
m
q
B
=
1
s
−
1
.
Assume that the loop rolls without slipping while in contact with the ramp.
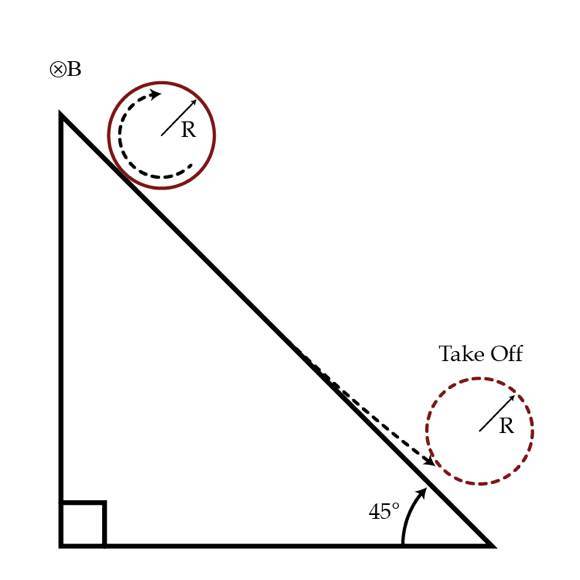
The answer is 2.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
The magnetic force in the motion can be decomposed in two: one in relation to translational motion and one in relation to rotational motion.
In the rotational motion, the force on each point of the ring has the same module and all of them are in direction to the center of the ring, because of it, the resultant magnetic force in relation to rotational motion is equal to zero.
In the translational motion, the resultant force can be written as:
F m = q v c . m B , where v c . m is the velocity of the center of mass.
The ring will lose touch with the ramp when F m = m g c o s 4 5 ° ,so:
q v c . m B = m g c o s 4 5 ° ⇒ v c . m = q B m g c o s 4 5 ° .
Analysing the torques in relation to I.C.R (Instantaneous center of rotation),which is the point where the ring touches the ramp, we have:
τ = I i . c . r α = m g s i n 4 5 ° × R , where α is the angular acceleration.
m
g
s
i
n
4
5
°
×
R
=
(
I
c
.
m
+
m
R
2
)
R
a
c
.
m
→
m
g
s
i
n
4
5
°
×
R
=
(
m
R
2
+
m
R
2
)
R
a
c
.
m
⇒
a
c
.
m
=
2
g
s
i
n
4
5
°
.
Since v f = v o + a t so:
q B m g c o s 4 5 ° = 0 + 2 g . s i n 4 5 ° t ⇒ t = 2 s
Consider when the speed and acceleration of the loop's center are v and a respectively.
The loop takes off when: q
B
v = m
g
cos(alpha) or v = m
g
cos(alpha)/(q*B)
Choose tangential point with the ramp as instantaneous rotation center, then the loop's moment of inertia is I = 2 m r^2. So m g r sin(alpha) = 2 m r^2 (a/r) or a = g*sin(alpha)/2
So t* = v/a = 2 m/(q B*tan(alpha)) = 2 (s)
When the loop rolls within slipping , v will be high enough to balance the component of gravitational force due to mass m that keeps the loop in contact with the ramp, then Normal reaction becomes 0.
then :
Bqv = m g sin 45 v = (m/B q) (g / √2) v = 1 * g/√2) = g/√2
use translation
mg/√2 - f = m a rotasi: f R = I alfa f R = m R^2 a/R f = m a m g /√2 - ma = ma a = g / (2√2) vt = vo + at g/√2 = (g/(2√2)) t t = 2 second
Let us start by determining the magnetic force acting on the charged loop. We claim that the total magnetic force acting on the loop is simply F M = q v C M × B where v C M is the velocity of the center of mass of the loop. In other words, the fact that the loop is rotating has no influence on the total magnetic force. To elucidate this point, we will decompose the motion of the loop into rotational and translational motion. Thus, the velocity of any point of the loop can be written as v = v C M + ω × r where r is the position of the point, relative to the loop's center of mass. Then, the total magnetic force can be written as F M = ∫ ( v C M + ω × r ) × B d q = q v C M × B + ∫ ( ω × r ) × B λ d s where λ is the charge per unit length. One can convince himself/herself that the second term of the above expression is zero if B is constant. Now, from Newton's second law (see the free-body diagram below) we have that m g sin ( α ) − f = m a and F N + q v C M B − m g cos ( α ) = 0 where f is the force of friction and F N the normal force. In addition we have the torque equation τ = f R = I α with α = R a (rolling without slipping) . Here, it is important to notice that the magnetic force does not produce torque with respect to the center of mass of the loop. Knowing that for a loop I = m R 2 we find that a = 2 g sin ( α ) → v C M ( t ) = 2 g sin ( α ) t . The loop takes off when F N = 0 which implies q v C M B = m g cos ( α ) . Thus, we obtain the time t ∗ = 2 q B / m cot ( α ) = 2 s .
Firstly, let’s analyse the electromagnetic force due to the magnetic field B exerted on the loop, which is rolling down the ramp with velocity v without slipping.
In the frame of the centre of mass of the loop, every single point on the loop has a velocity tangential to the loop with the magnitude of v . Let this velocity be v 1 . The centre of mass of the loop is moving with a velocity parallel to the ramp, with the same magnitude of v . (This is because the question assumes the loop is rolling without slipping all the time when in contact with the ramp. The velocity at the point of contact between the loop and the ramp in the inertial frame is thus 0.) Let the velocity of the centre of mass be v 2 . Hence, in the inertial frame, the velocity of a point on the loop is v = v 1 + v 2 .
The electromagnetic force exerted on the loop, F = ∫ ( v × B ) d q = ∫ v 1 × B d q + ∫ v 2 × B d q
Since the charge is distributed uniformly in the loop, the term involving the integral of v 1 is 0. Hence F = ∫ v 2 × B d q = q ( v 2 × B ) . This shows the force has the magnitude of q v B , and is always in an upward direction perpendicular to the ramp.
When the charged loop is moving down the ramp, besides the electromagnetic force, it experiences two forces, its weight, m g and the friction of the ramp, f .
Let the angle of the ramp be θ = 4 5 ∘ to the horizontal.
Equation of linear motion: m a = m g sin θ − f
Equation of rotational motion: f R = I α = m R 2 α , where I is the moment of inertia of the loop, and α is the angular acceleration. Since it rolls without slipping, α = R a
⟹ f = m a
⟹ m a = m g sin θ − m a
⟹ a = 2 1 g sin θ
Hence, v = a t = 2 1 g sin θ t , and F = 2 1 q B g sin θ t
When the loop “takes off”, i.e. the normal force on the loop is 0, F = m g cos θ
⟹ 2 1 q B g sin θ t = m g cos θ
⟹ t = q B sin θ 2 m cos θ = 2 s