Magnetics with polygon

Relevant wiki: Magnetic Effects of Current

After converting the wire as required, we would get a $n$ sided regular polygon of side length $\dfrac{l}{2n}$ such that the perpendicular distance of the center from each of the sides is equal to its inradius which would be $\dfrac{l}{2n} \cot{\left( \dfrac{pi}{n} \right)}$ .
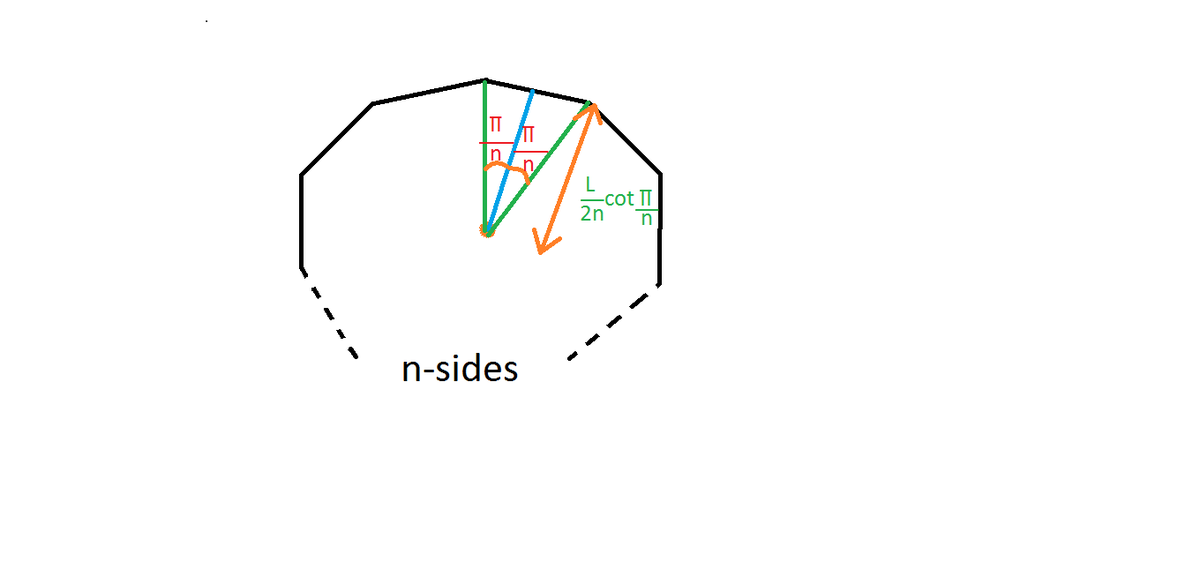We observe that the magnetic field produced at the center by all the side lengths would be in the same direction by right hand thumb rule.
Applying the formula for magnetic field produced by a finite wire = $\dfrac{\mu_{0} I}{4 \pi d} \left(\sin{(C)} + \sin{(D)}\right)$ .

$\begin{aligned} B & = \dfrac{\mu_{0} I}{4 \pi \frac{l}{2n} \cot{\left(\frac{\pi}{n}\right)}} \left(sin{\left(\dfrac{\pi}{n}\right)} + sin{\left(\dfrac{\pi}{n}\right)} \right) \\ \\ B_{\text{net}} = n \times B & = \dfrac{\mu_{0} I n^2 \sin{\left(\frac{\pi}{n}\right)}}{\pi l \cot{\left(\frac{\pi}{n}\right)}} \end{aligned}$

Now, plugging in $I = 5 A$ , $L = 2 m$ , $n = 15$ and $\mu_{0} = 4 \pi \times {10}^{-7}$ , we get:-
$B_{\text{net}} = {\color{#3D99F6}{\boxed{9.94}}} \mu T$