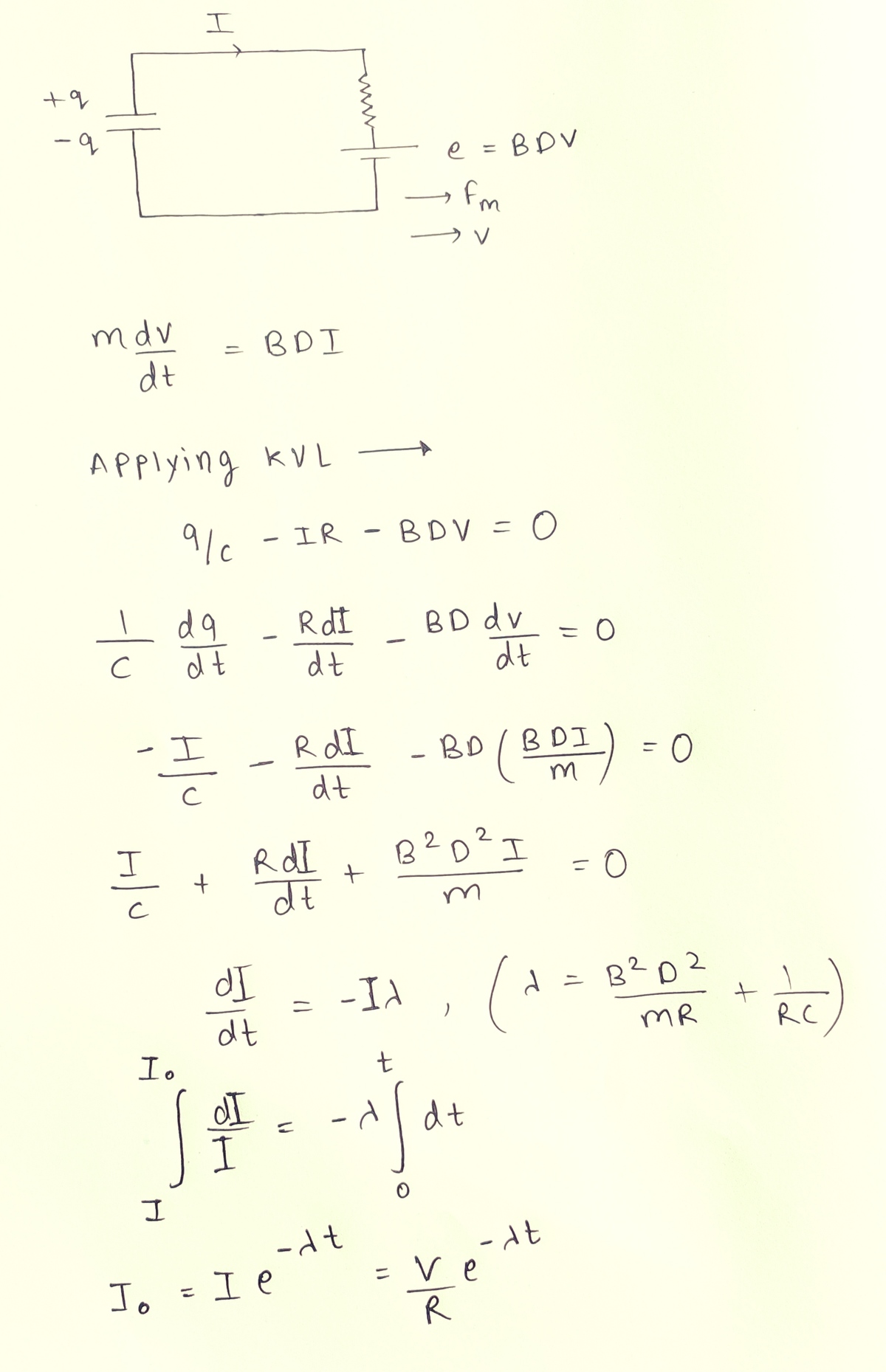Magnetism and Capacitor Story
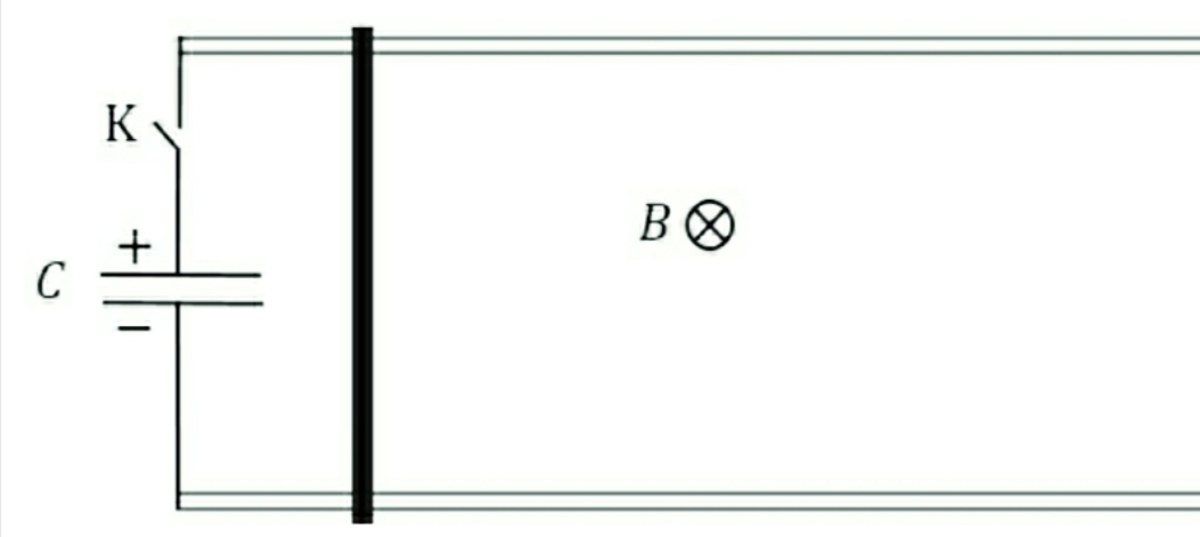
A pair of long parallel metallic rails of negligible resistance and separation
D
are placed horizontally. A horizontal metal rod (dark thick line) of mass
m
and resistance
R
is placed perpendicularly onto the rails at one end(as shown). A uniform magnetic field
B
exist perpendicular to the plane of paper (pointing into the page).One end of the rail track is connected to a key
(
K
)
and a capacitor of capacitance
C
charged to voltage
V
. At
t
=
0
the key is closed. Neglect friction and self inductance of the loop.
 Find the final speed
V
F
i
n
a
l
attained by the rod
.
If your answer comes in the form of
V
F
i
n
a
l
=
m
+
J
B
N
d
X
C
F
B
D
C
V
.
Type your answer as
F
+
N
+
X
+
J
.
F
,
N
,
X
,
J
are integers
.
Find the final speed
V
F
i
n
a
l
attained by the rod
.
If your answer comes in the form of
V
F
i
n
a
l
=
m
+
J
B
N
d
X
C
F
B
D
C
V
.
Type your answer as
F
+
N
+
X
+
J
.
F
,
N
,
X
,
J
are integers
.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice problem.
Conceptually, the following is what is happening. At t = 0 when the switch closes, the capacitor begins to discharge. Since a resistor is present, the discharge will not be instantaneous. So the discharging current will begin to flow in a clockwise manner. As the current flows through the rod of length D , a voltage will be induced in the rod as per Faraday's law. Let us break this down into mathematical steps as follows.
At an arbitrary time t , let the charge on the capacitor be Q and the current through the circuit be I . SInce it is a discharging current flowing clockwise, we have:
Q ˙ = − I … ( 1 )
Now applying Kirchoff's voltage law to the circuit gives:
V i n d u c e d − I R + C Q = 0 … ( 2 )
Now, looking at the dynamics of the rod, since the current flows clockwise, it flows down along the rod. The rod, as a result, experiences a magnetic force acting to the right, with magnitude:
F = I D B
Let the velocity of the rod be v . Applying Newton's second law:
m v ˙ = I D B … ( 3 )
Say the rod has moved a distance x from the left end at time t . The magnetic flux through the rectangular circuit is:
ϕ = B D x
Now, applying Faraday's law gives:
V i n d u c e d = − ϕ ˙ = − B D v … ( 4 )
Now, looking at equation 3 , we see that:
m v ˙ = I D B ⟹ m v ˙ = − Q ˙ D B
at t = 0 , I assume that the rod is at rest and the capacitor voltage is V . By integrating the above equation and applying initial conditions, one gets:
m v = C V B D − Q B D … ( 5 )
Looking at equation 2 , it can be re-written as:
V i n d u c e d − I R + C Q = 0 ⟹ − B D v − I R + C Q = 0
Replacing equation 3 above gives:
⟹ − B D v − B D R m v ˙ + C Q = 0
Replacing Q with equation 5 above gives:
− B D v − B D R m v ˙ + B D C C V B D − m v = 0
Now, at steady state, the acceleration v ˙ becomes zero and the velocity reaches its final value. Performing this step in the above equation, and solving, gives the final velocity which is:
v f i n a l = m + C B 2 D 2 C V B D
A couple of suggestions:
- Add the fact that the rod is initially at rest to the problem statement.
You can make one or more follow up problems based on this.
-
Asking for the total amount of heat dissipated in the resistor.
-
Asking to derive the velocity as a function of time.
-
The introduction of an inductor to the problem.
-
A similar problem where the magnetic field is time-varying.
Log in to reply
@Karan Chatrath Sir @NJ STAR has posted a solution in which he calculate velocity as a function of time .