Magnetism Exercise (06-08-2020)
A particle of mass
m
and charge
+
q
enters horizontally with speed
v
0
midway between the horizontal plates of a parallel plate capacitor at time
t
=
0
. Separation between tha capacitor plates is
d
and it starts getting charged, by a constant current source, at time
t
=
0
. Plate area of capacitor is
A
. It was found that the particle just misses (to hit) the lower plate.
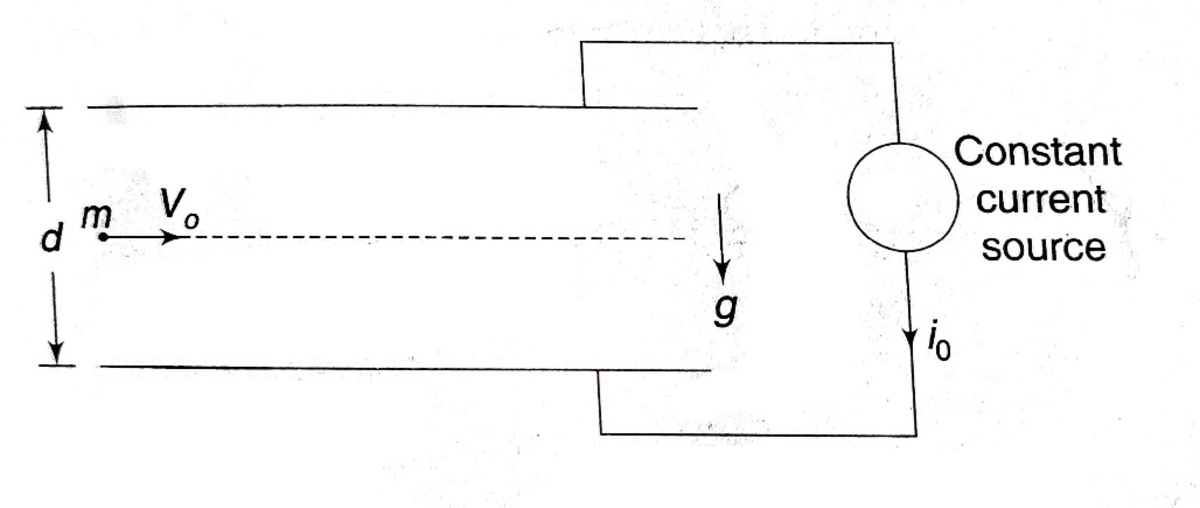
Assume that the plates are quite long and acceleration due to gravity is g .
Find the constant current
i
0
supplies by the source to the capacitor.
If your answer comes in the form of
i
0
=
α
q
d
m
g
1
.
5
A
ϵ
0
Type your answer as
α
.
Details and Assumptions
1)
Consider no magnetic force on charge.
The answer is 1.154.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Foolish Learner why did you changed your name??
Log in to reply
Because I don't think I am learned enough.
Log in to reply
@Foolish Learner WHAT! , then what about me. If you didn't learned enough, then in that perspective I am not yet born.
In the professional community you may not be learned enough, but for a 60+ year old man who is just learning mathematics, you are truly smarter and sharper than all of us. Your perseverance and sharpness is admirable, sir.
I applaud you, Mr. Bhattacharjya.
"Do not go gentle into thy good night
Rage, rage, against the dying of the light"
@Foolish Learner can you post analytical solution of this problem https://brilliant.org/problems/magnetism-exercise-09-08-2020/ Thanks in advance.
Consider a coordinate frame to be placed at the point of projection (Y-Axis upwards and X axis to the right)
Let the charge on the capacitor at time t be Q and since it is a constant current source:
Q = i o t
The electric field between the plates is:
E = A ϵ o Q = A ϵ o i o t
The X and Y components of acceleration of the particle are:
x ¨ = 0 y ¨ = − g + A ϵ o m i o t q
Solving:
x ˙ = v o y ˙ = − g t + 2 A ϵ o m i o t 2 q
x = v o t y = − 2 g t 2 + 6 A ϵ o m i o t 3 q
Having solved the Y-motion, if the particle must just miss the bottom of the plate, it's minimum value must be y m i n = − d / 2 . This essentially means that that happens at the time when:
y ˙ = 0
Solving for time one gets:
t o = i o q 2 A ϵ o m g
Finally, using the above expression:
y ( t ) = − 2 g t 2 + 6 A ϵ o m i o t 3 q
− 2 d = y ( t o )
Finally, i o can be solved for and the resulting expression is (simplifications left out):
i o = 3 2 ( q d m g 1 . 5 A ϵ o )
@Karan Chatrath
in the fourth step according to me it should be
m
a
y
=
m
g
−
A
ϵ
0
q
i
0
t
After that we can cancel
m
What do you think?
Log in to reply
It depends on how you define the coordinate axes. I chose the Y-axis to be facing upwards (see the first line of my solution). According to your equation, your Y-axis points downwards.
@Karan Chatrath
did you have solved this problem,

I have posted that some days before.
If not, can you guide me 3-4 steps how to start, I. Will be grateful, thanks in advance.
Log in to reply
This is a very nice problem. I will post a note on this. Later, though.
Start by applying Newton's second law as the particle slides along the incline and see under what conditions the particle will lose contact with the incline. The instant when the particle loses contact is the initial condition for the cycloidal motion. Apply Newton's law and then derive the equation of the cycloid by solving the differential equations. The amplitude of that cycloid will be h which will be related to the initial conditions of the cycloidal motion. Using that, you can find the relation for l
Log in to reply
@Karan Chatrath
I am still stucking in the problem.
I have already posted the problem
here
You can post it's solution, if it takes time to write latex, just use pen and. Page.
Thanks in adavnce.
Capacitance of the plates is
C = d ϵ 0 A
Potential difference between the plates is
V = ϵ 0 A i 0 t d
Force acting on the charge due to the electric field in the region between the plates is
F = d q V = ϵ 0 A i 0 q t acting vertically upwards.
The downward acceleration of the charge is
d t d v = g − ϵ 0 m A i 0 q t
⟹ v = g t − 2 ϵ 0 m A i 0 q t 2
The charge will just miss hitting the lower plate if at this point the vertical component of it's velocity is zero, which will happen at time
t 0 = i 0 q 2 ϵ 0 m A g
Then,
2 d = ∫ 0 t 0 v d t = 3 2 i 0 2 q 2 ϵ 0 2 m 2 A 2 g 3
⟹ i 0 = 3 4 q d ϵ 0 m A g 2 3
Therefore α = 3 4 ≈ 1 . 1 5 4 .