The Field Keeps Me Down
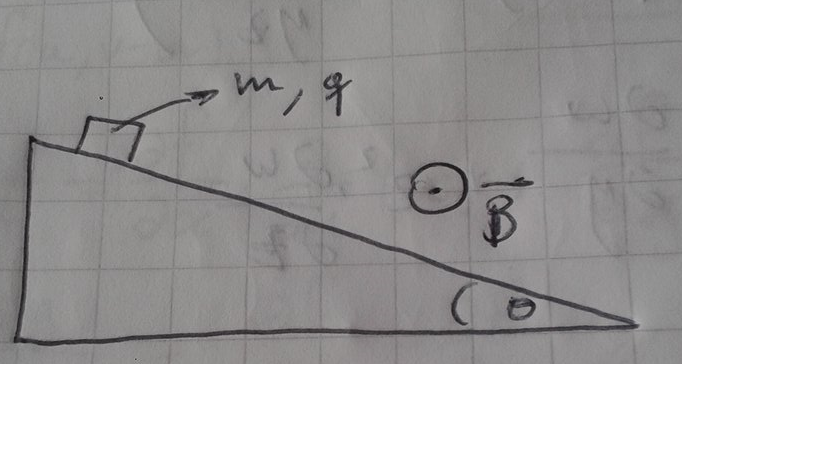 An object with mass
and charge
is dropped on an infinite inclined plane which forms an angle
with the horizontal, in the presence of a constant magnetic field
which goes out the page. If the coefficient of friction between the plane and the object is
, the maximum magnetic force can be written as
, find the value of
An object with mass
and charge
is dropped on an infinite inclined plane which forms an angle
with the horizontal, in the presence of a constant magnetic field
which goes out the page. If the coefficient of friction between the plane and the object is
, the maximum magnetic force can be written as
, find the value of
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Lorentz force law (mixed fields)
With the FBD we can find out that the magnitude of the normal is given by: N = c o s ( θ ) ⋅ m g + q B 0 x ˙ Then, the value of the friction force equals: ∣ f r ∣ = μ ( c o s ( θ ) ⋅ m g + q B 0 x ˙ ) So the net force, using the Newton's Second Law of Motion , will give us the next differential equation: m x ¨ = s i n ( θ ) ⋅ m g − μ ( c o s ( θ ) ⋅ m g + q B 0 x ˙ ) x ¨ + m μ q B 0 x ˙ = g ( s i n ( θ ) − μ c o s ( θ ) ) Which gives us as solution for the velocity: x ˙ = μ q B 0 m g ( s i n ( θ ) − μ c o s ( θ ) ) ( 1 − e − m μ q B 0 t ) As the magnetic force, by Lorentz Law , is proportional to the velocity, the maximum magnetic force will be reached at the moment of maxmum velocity, which is x ˙ m a x = μ q B 0 m g ( s i n ( θ ) − μ c o s ( θ ) ) . So the maximum magnetic force equals: F B m a x = μ m g ( s i n ( θ ) − μ c o s ( θ ) ) Then: s i n 2 ( θ ) + c o s 2 ( θ ) = 1