Magnetism + Sequence = Maquence

Electricity and Magnetism Level 5

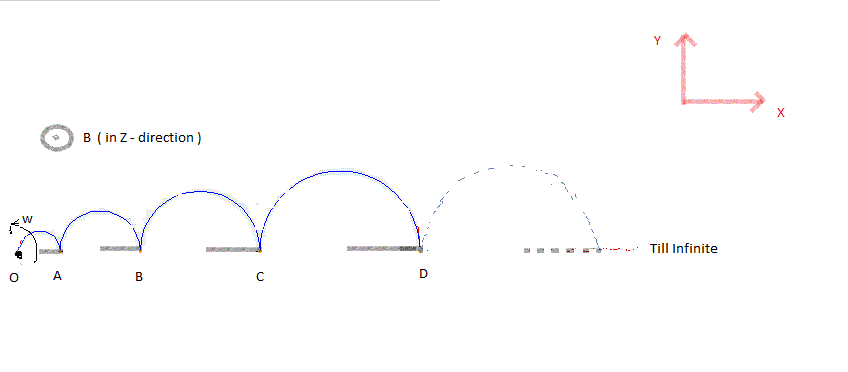An infinitely long, thin, conducting rod is bent in the form of semi-circular rings, as shown in the figure. Now it is placed in a uniform magnetic field of magnitude $B_0$ oriented perpendicular to the plane of the rings.

The radii of the successive half rings are as follows: $R, 3R^2,5R^3,7R^4 \ldots \infty$

Now if we rotate the Rod about the point $O$ with constant angular velocity $\omega$ , find the magnitude of the induced emf developed in the rod.

Assumptions

The rod is very thin.
The rod is rigid.

Details

$B _0=2.0$ Tesla
$\omega =5$ rad/sec
$R=0.5$ m

This is Original

Try more mixing of concepts

The answer is 180.

2 solutions

Deepanshu Gupta
Oct 10, 2014

This system is Analogous To an rod rotating with angular velocity ' $\omega$ .' and has Length equal to sum of diameters of all rings. Let it's Length is 'L' then $L=2\quad (R\quad +{ \quad 3R }^{ 2\quad }+\quad { 5R }^{ 3 }\quad +\quad { 7 }R^{ 4 }\quad ..............\quad \infty )\quad \quad \longrightarrow (1)\\ RL=\quad \quad \quad \quad \quad 2({ R }^{ 2\quad }+\quad \quad { 3R }^{ 3 }\quad +\quad { 5R }^{ 4 }\quad ..............\quad \infty )\quad \quad \longrightarrow (2)\\ \\ \Rightarrow \quad (1-R)L=\quad 2(R\quad +\quad { \quad 2R }^{ 2\quad }+\quad { 2R }^{ 3 }\quad +\quad { 2 }R^{ 4 }\quad ..............\quad \infty )$ .

Now it is GP $After$ $Second$ $Term$ so it's sum can be determined easily Therefore:

$L=\frac { 2R(1+R) }{ { (1-R) }^{ 2 } }$ .

Now Total emf induced can be written as:

$\Rightarrow { E }_{ ind }=\frac { 1 }{ 2 } B\omega ({ L }_{ eff }^{ 2 })\\ \Rightarrow { L }_{ eff }=\frac { 2R(1+R) }{ { (1-R) }^{ 2 } } \\ \Rightarrow {E }_{ ind }=2B\omega \quad { { (\frac { R(1+R) }{ { (1-R) }^{ 2 } } ) }^{ 2 } }$ .

Now Put The Values and Get The Answer.

$ANS=180$ .

There is one more method to solve it namely that we can imagine rods being placed at the place of diameters and as it is a rigid body, we can find the successive increase in potential and sum it to get a G.P. But, we don't get the same answer. So, how is one method more "right" than the other. This solution or Leff one?

Tushar Gopalka - 6 years, 6 months ago

That is also Correct Method ! And Also give same answer But In that case you can't use directly that :

$\displaystyle{{ E }_{ k }\quad \neq \quad \cfrac { B\omega }{ 2 } { L }_{ k }^{ 2 }\quad }$ .

Because when yo derived this relation by integration then You must have to put limits from the point about which system is rotated !!

For eg: Emf between ${ K }^{ th }$ Rod is given by ;

$\displaystyle{{ E }_{ k }\quad =B\omega \int _{ a }^{ b }{ xdx } }$ .

where :

$\displaystyle{a\quad =\quad 2\sum _{ n=1 }^{ n=K-1 }{ (2n-1){ R }^{ n } } }$ .

$\displaystyle{b\quad =\quad 2\sum _{ n=1 }^{ n=K }{ (2n-1){ R }^{ n } } }$ .

So this also give same Answer!

@Tushar Gopalka

Deepanshu Gupta - 6 years, 6 months ago

Yeah..that's what I was saying that we should arrive at the same answer using both the methods.....Probably made some mistake in calculations...

Tushar Gopalka - 6 years, 6 months ago

Thanks @Deepanshu Gupta for pointing out the key point in the alternate approach. I also did the same mistake.

raj abhinav - 1 year, 2 months ago

My calculation !! Darn it !

Keshav Tiwari - 6 years, 5 months ago

The problem is good but overrated

mudit bansal - 6 years, 4 months ago

Jaivir Singh
Feb 20, 2015

Eind = 1/2Bl2w = 180 volt

Magnetism + Sequence = Maquence

This is Original

Try more mixing of concepts

The answer is 180.

2 solutions

0 pending reports