Magnetism Series #2
In a gravity free region, a
-shape rigid insulating frame is rotating in its plane about the end of the central bar of length
with a constant angular velocity
A strong uniform and static magnetic field of induction
exists everywhere pointing into the plane of the frame. Two indentical beads
and
each of mass
and charge
can slide without friction on the frame.
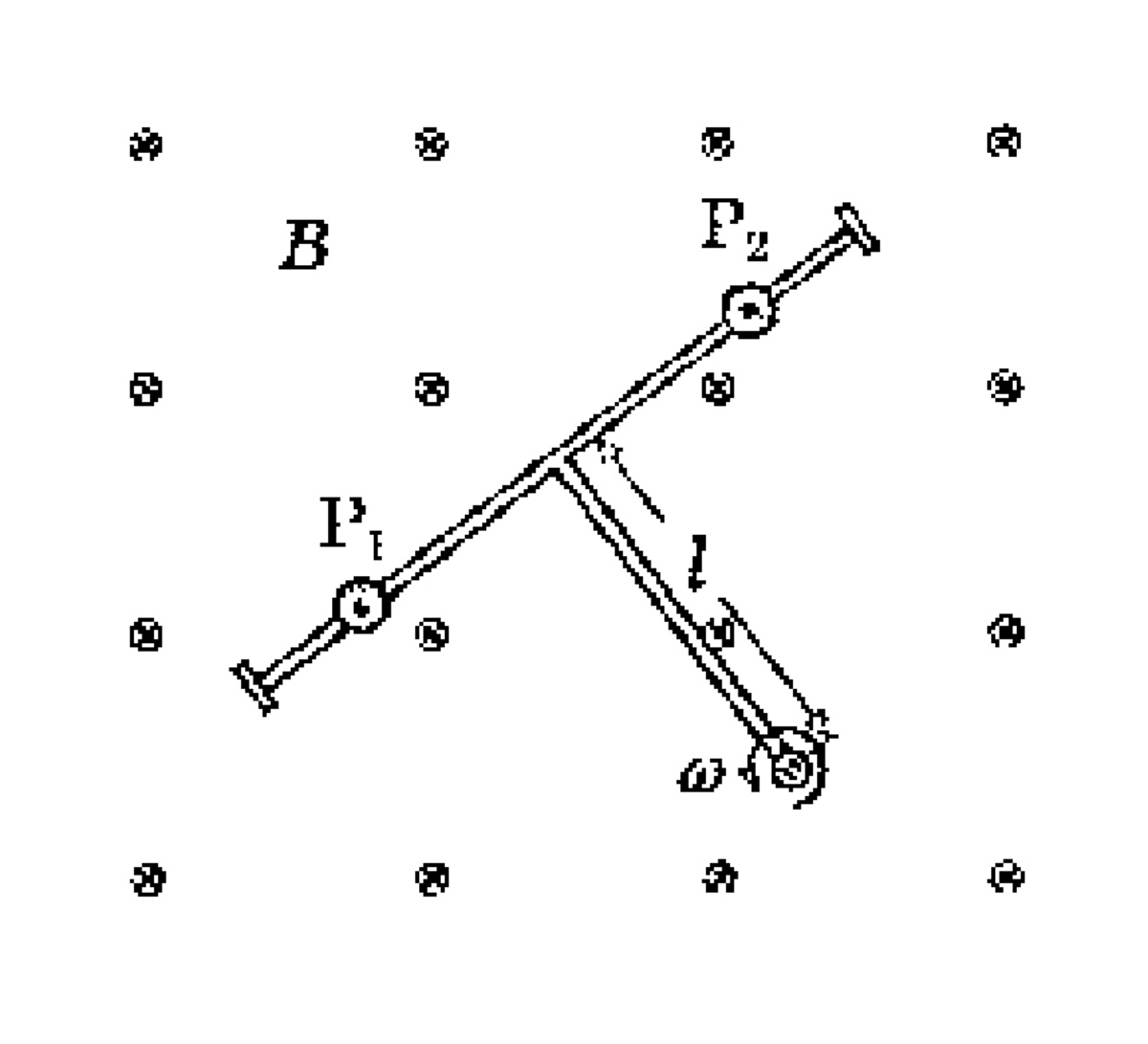
Find the equilibrium position of the beads relative to the frame .
is the angular position of the beads measured from the central rod.
Type your answer as
The problem is taken from my Physics Book.
Thanks in advance if you are going to post solution.
The answer is 21.333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Assume that the rod is hinged at the origin and that the central rod lies in the first quadrant. Let the coordinates of each of the charged particles be ( x 1 , y 1 ) and ( x 2 , y 2 ) respectively. Let the distance of each of the charges be r from the central rod along the perpendicular rod. The coordinates of the particles are then:
x 1 = L cos ( ω t ) + r sin ( ω t ) y 1 = L sin ( ω t ) − r cos ( ω t )
r 1 = x 1 i ^ + y 1 j ^ v 1 = d t d r 1 a 1 = d t d v 1
x 2 = L cos ( ω t ) − r sin ( ω t ) y 2 = L sin ( ω t ) + r cos ( ω t )
r 2 = x 2 i ^ + y 2 j ^ v 2 = d t d r 2 a 2 = d t d v 2
The forces acting on each of the particles are the electrostatic force along the perpendicular rod, the magnetic force and the reaction force due to the rod (directed along the central rod. The electrostatic force on one of the charge 1 is:
F e = 4 r 2 K q 2 ( sin ( ω t ) i ^ − cos ( ω t ) j ^ )
The magnetic force on charge 1 is:
F b = q ( v 1 × ( − B k ^ ) )
The magnitude of the reaction force on charge 1 is N 1 . The reaction force vector is:
F r 1 = N 1 ( cos ( ω t ) i ^ + sin ( ω t ) j ^ )
Finally, applying Newton's second law for charge 1 gives:
m a 1 = F e + F b + F r 1
Plugging in all expressions and separating the x and y components of the force gives us two equations. Using these two equations, one can solve for two unknown variables which are N 1 and r ¨ . After a lot of simplification, the expression for r ¨ comes out to be:
r ¨ = 4 m r 2 K q 2 − 4 B q r 3 ω + 4 m r 3 ω 2
Looking at the above expression, the particle achieves equilibrium when r ¨ = 0 . This means:
K q 2 − 4 B q r 3 ω + 4 m r 3 ω 2 = 0 ⟹ r 3 = 1 6 π ϵ o ω ( q B − m ω ) q 2 ⟹ r = ( 1 6 π ϵ o ω ( q B − m ω ) q 2 ) 1 / 3
Now to find the angle θ , simple trigonometry can be applied to obtain the expression:
tan θ = L r ⟹ tan θ = ( 1 6 π ϵ o ω L 3 ( q B − m ω ) q 2 ) 1 / 3
These problems are not difficult but are very tedious to work out. As an exercise for yourself, do the same steps for charge 2. You should get the same expression for r ¨ when you do so.