Magnetism Series #6

A uniform dielectric hollow cylinder of mass $M$ and radius $R$ , length $l$ carrying uniform charge of surface charge density $\sigma$ can rotate without friction about a fixed horizontal axle that coincides with the axis of the cylinder. Several turns of a light thin insulating cord are wrapped on the cylinder and a block of mass $m$

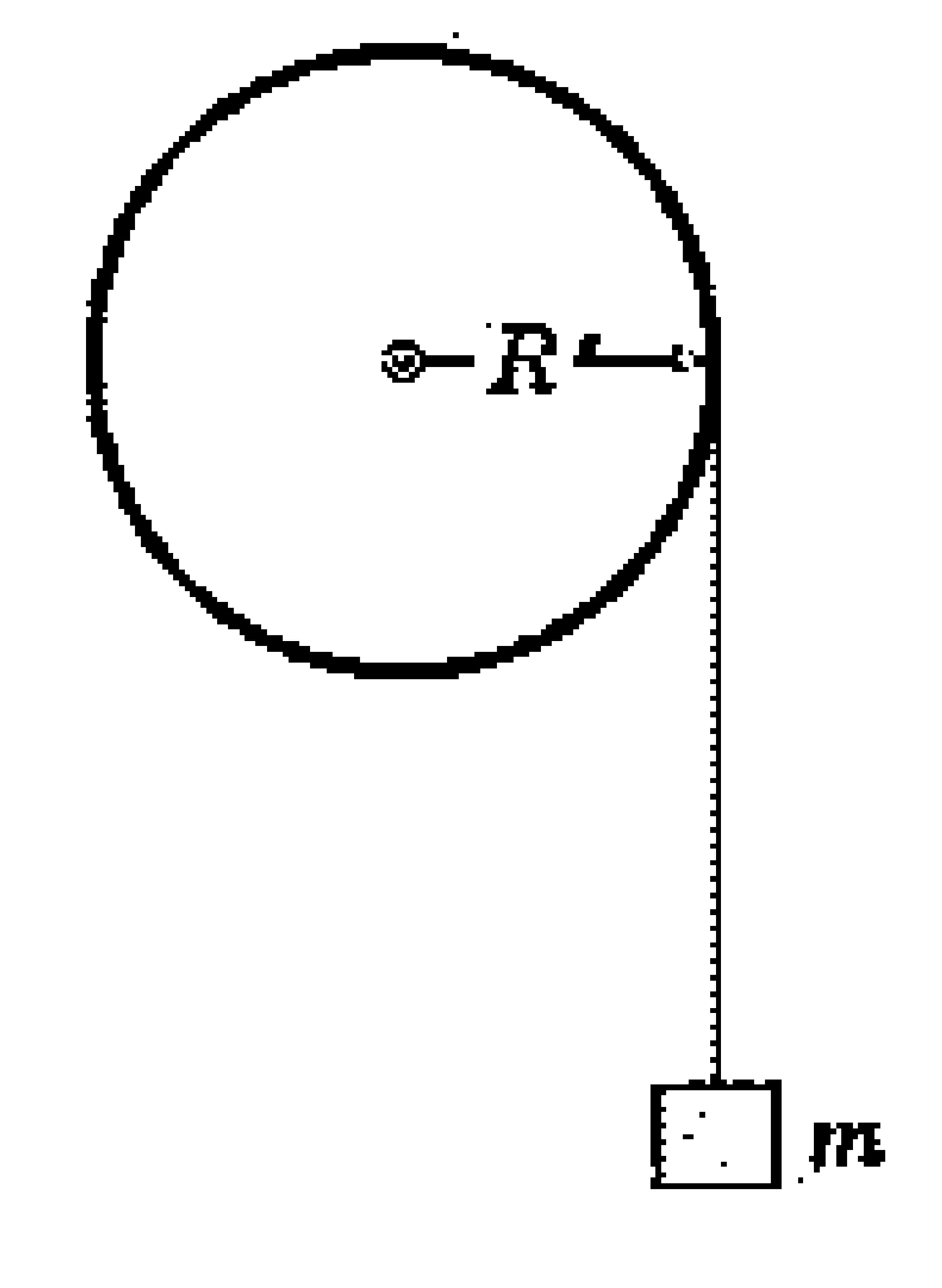
is suspended from the free end of the cord. Initially the block is held at rest as shown in the figure. Find acceleration of the block after it is released. Neglect charge transferred to the cord and fringing of magnetic field at the ends of the cylinder.

Acceleration due to gravity is $g$ and permeability of the medium inside the cylinder is $\mu_{0}$

Answer comes in the form of $a=\frac{\alpha mg}{\beta m +\gamma M+\delta \mu_{0}\sigma ^{\phi} R^{\lambda} l}$

Type you answer as $\alpha+\beta+\gamma+\delta+\phi+\lambda=?$

The problem is taken from my Physics Book.

Thanks in advance if you are going to post solution.