Magnitude of magnetic field inside a star shaped wire

I used computational Biot-Savart. Python code is below. Note that the code is general enough to compute the magnetic field at any point within 3D space, but this would require computation of all twelve edges individually, instead of calculating one pair of edges and multiplying by 6.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151

import math

u0 = 2.7  # pick junk values for u0,I
I = 0.6

ang1 = math.pi/3.0
ang2 = 0.0

x1 = math.cos(ang1) # hexagon vertex at 60 deg (see diagram)
y1 = math.sin(ang1)

x2 = math.cos(ang2) # hexagon vertex at 0 deg (see diagram)
y2 = math.sin(ang2)

vx = x1 - x2  # vector between two vertices
vy = y1 - y2

alpha = -x1/vx

xp = 0.0                # Highest point of star = (xp,yp)
yp = y1 + alpha*vy 

#4a = 2*yp

a = yp/2.0 # Parameter "a" in relation to yp

##################################################

Bx = 0.0  # Initialize magnetic field
By = 0.0
Bz = 0.0

Bmult = u0*I/(4.0*math.pi)    # Biot Savart multiplier
ansmult = u0*I/(4.0*math.pi*a) # answer format multiplier

xref = 0.0  # Take center of loop as reference
yref = 0.0
zref = 0.0

##################################################

# Magnetic field from light blue edge - use Biot-Savart

xst = x1   # start point
yst = y1
zst = 0.0

xend = xp # end point
yend = yp
zend = 0.0

N = 10**6

dx = (xend - xst)/N
dy = (yend - yst)/N
dz = (zend - zst)/N

x = xst
y = yst
z = zst

for j in range(0,N):

    rx = x - xref
    ry = y - yref
    rz = z - zref

    rcube = (rx**2.0 + ry**2.0 + rz**2.0)**(3.0/2.0)

    crossx = dy*rz - dz*ry
    crossy = -(dx*rz - dz*rx)
    crossz = dx*ry - dy*rx

    dBx = Bmult * crossx / rcube
    dBy = Bmult * crossy / rcube
    dBz = Bmult * crossz / rcube

    Bx = Bx + dBx
    By = By + dBy
    Bz = Bz + dBz

    x = x + dx
    y = y + dy
    z = z + dz

##################################################

# Magnetic field from dark green edge - use Biot-Savart

xst = xp # start point
yst = yp
zst = 0.0

xend = -x1 # end point
yend = y1
zend = 0.0

N = 10**6

dx = (xend - xst)/N
dy = (yend - yst)/N
dz = (zend - zst)/N

x = xst
y = yst
z = zst

for j in range(0,N):

    rx = x - xref
    ry = y - yref
    rz = z - zref

    rcube = (rx**2.0 + ry**2.0 + rz**2.0)**(3.0/2.0)

    crossx = dy*rz - dz*ry
    crossy = -(dx*rz - dz*rx)
    crossz = dx*ry - dy*rx

    dBx = Bmult * crossx / rcube
    dBy = Bmult * crossy / rcube
    dBz = Bmult * crossz / rcube

    Bx = Bx + dBx
    By = By + dBy
    Bz = Bz + dBz

    x = x + dx
    y = y + dy
    z = z + dz


##################################################

# Print B-field, normalized by answer multiplier
# Multiply by 6 because there are six star points
# Only z-component is non-zero

print (6.0*Bx/ansmult)
print (6.0*By/ansmult)
print (6.0*Bz/ansmult)
print ""
print ""

# Print answer options
# First option matches calculation

print 6.0*(math.sqrt(3.0)-1.0)
print 6.0*(math.sqrt(3.0)+1.0)
print 3.0*(math.sqrt(3.0)-1.0)
print 3.0*(-math.sqrt(3.0)+2.0)

The way I solved it was by superposition.

Consider the star as two overlapping large triangles (upper and lower pointing) with currents going in one direction, and a smaller hexagon that subtracts the inner segments as current that goes the opposite direction.

The neat part is the perpendicular distance to the center is always $a$ for all the segments. Just find the contribution from the longer segment minus the shorter segment and times 6 by hexagonal symmetry:

$B = -6\cdot \frac{\mu_0 I}{2\pi a}(\sin{\pi/6})$ for the small segments of the hexagon. $B = +6\cdot \frac{\mu_0 I}{2\pi a}(\sin{\pi/3})$ for the longer segments of the triangles.

Thus, the total would be $B = \frac{6\mu_0 I}{4\pi a}(\sqrt{3}-1)$ .

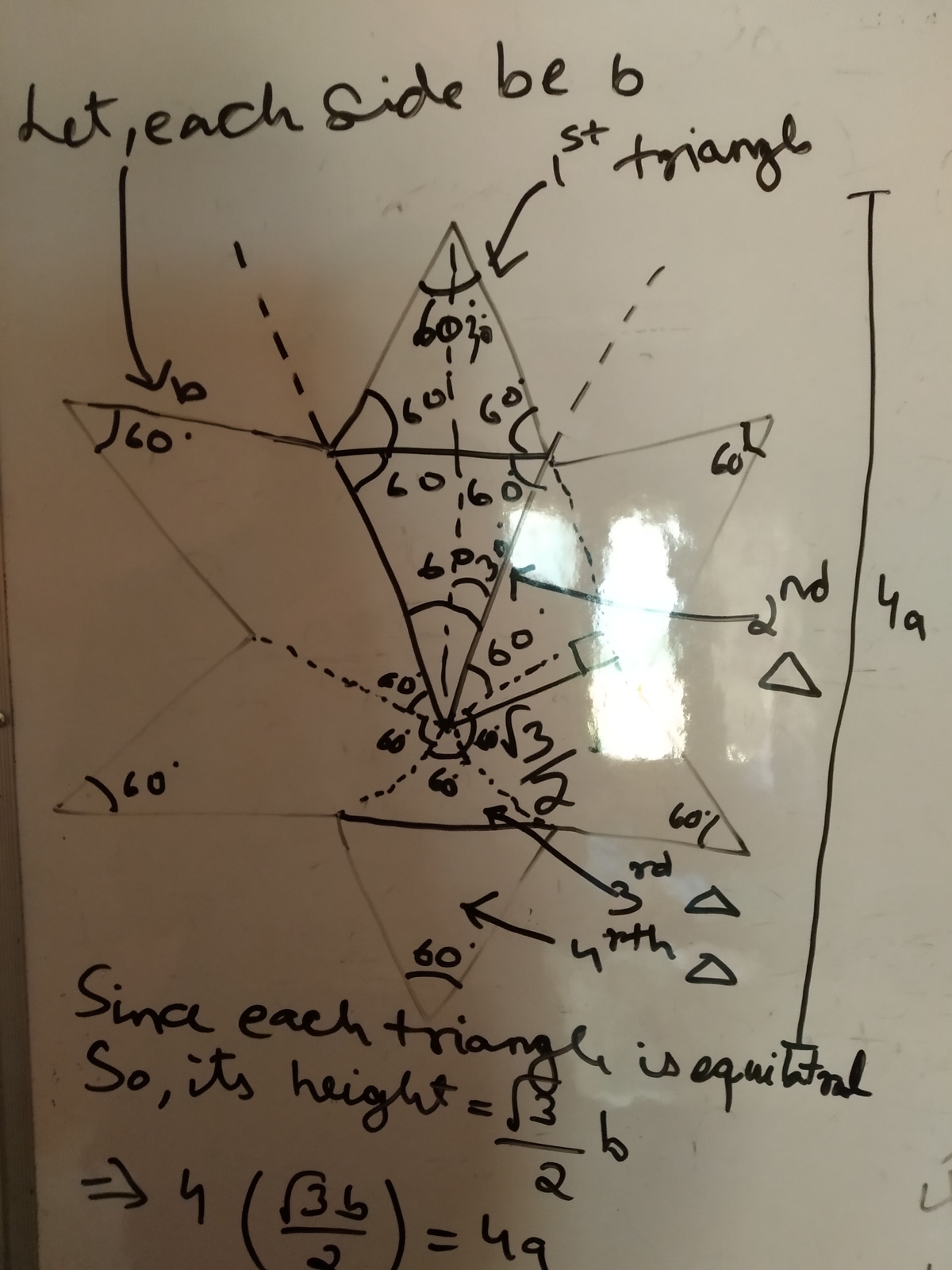
Here is the solution - its easy just used biot-savart law for one straight wire and multiplied with all 12 to get total