Maintaining the ratio

Number Theory Level 1

Robert solved some fraction problems on Brilliant and we have the following information.

  1. He attempted only 9 10 \frac{9}{10} of all the problems.
  2. He answered correctly only to 9 10 \frac{9}{10} of the attempted problems.

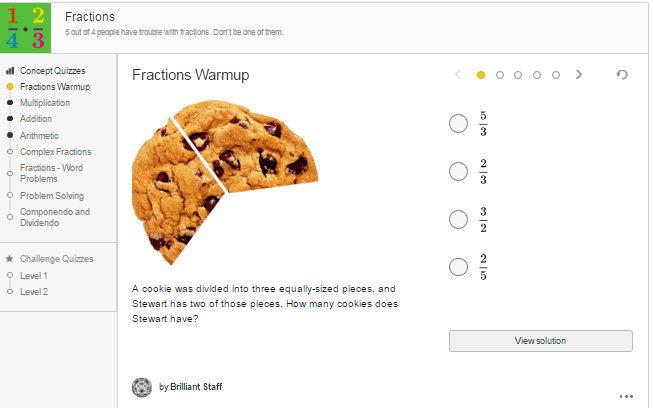
If he answered incorrectly to 18 problems, how many problems were there in all?


The answer is 200.

Sandeep Bhardwaj by Sandeep Bhardwaj , 28, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Mohammad Farhat
Aug 17, 2018

He only attempted 9 10 \dfrac{9}{10} of the problems

Multiply 9 10 \dfrac{9}{10} by 9 10 \dfrac{9}{10} . We get 81 100 \dfrac{81}{100}

We know that 9 10 \dfrac{9}{10} = 90 100 \dfrac{90}{100}

Subtract 81 100 \dfrac{81}{100} from 90 100 \dfrac{90}{100} . We get 9 100 \dfrac{9}{100} .

Given that 9 100 \dfrac{9}{100} = 18 problems

Dividing each side by 9, we get 1 100 \dfrac{1}{100} = 2 problems

Multiplying each side by 100, we get 100 100 \dfrac{100}{100} which is 1 = 200 problems

0 Helpful 0 Interesting 0 Brilliant 0 Confused

@Sandeep Bhardwaj , How do I join your classes? I really want to.

Mohammad Farhat - 2 years, 8 months ago

@Sandeep Bhardwaj , Can you please reply?

Mohammad Farhat - 2 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...