Pulley Challenge!
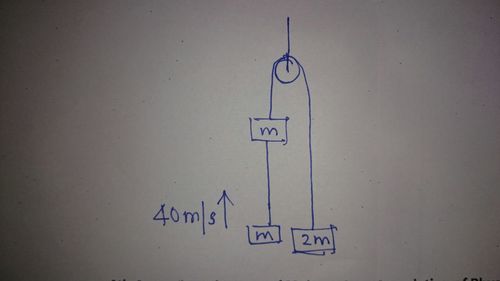 A mass of
kg is suspended from the string on one side while two masses of
kg are on the other side as shown.
A mass of
kg is suspended from the string on one side while two masses of
kg are on the other side as shown.
The system starts at rest. Suddenly, the lower mass of kg is flicked up with velocity 40 m/s.
After how many seconds will the rope be taut again?
Details
- Assume the rope is very long and the masses do not collide.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

As @satyen nabar said, when you flick the lower mass up, it'll stop pulling. System will lose the equilibrium, and the force on the left is less than on the right. There must be acceleration on the right.
Force from mass 2 m due to gravity g is 2 m g , and so the mass m with force m g .
From Σ F = m a
Resultant force 2 m g − m g = m g , pulls the mass 3 m downwards (right side), with acceleration a .
m g = ( 3 m ) a
Therefore, a = 3 g m / s 2
From s = u t + 2 1 a t 2
Consider the upper mass. Flicking the lower mass, neglecting how strong the rope is, doesn't affect the initial speed of the upper mass. Upper mass is pulled by right side with acceleration a = 3 g m / s 2 . Let t be amount of time between starting to flick and starting to taut.
s 1 = 2 1 ( 3 g ) t 2 __(1)
Consider the lower mass. Flicking the lower mass at initial speed 4 0 m / s , in a gravitational field, acceleration a = g m / s 2 , with time t .
s 2 = 4 0 t + 2 1 g t 2 __(2)
No matter where the masses are flicked or the ropes taut, the displacement between 2 masses are always the same, which means s 1 = s 2 .
(1) = (2); we get 2 1 ( 3 g ) t 2 = 4 0 t + 2 1 g t 2 .
Take g = 1 0 m / s 2 and solve the equation we get t = 6 s ~~~