Make your life colourful
In the figure A G = 2 cm , G B = 1 2 cm , B E = 3 cm , E C = 1 0 cm , C F = 4 cm , F A = 1 1 cm , If the area of shaded region can be expressed as G M Where both are co-prime to each other, then find M + G .
Note :The answer is not as sweet as M and G.
The answer is 18167773.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
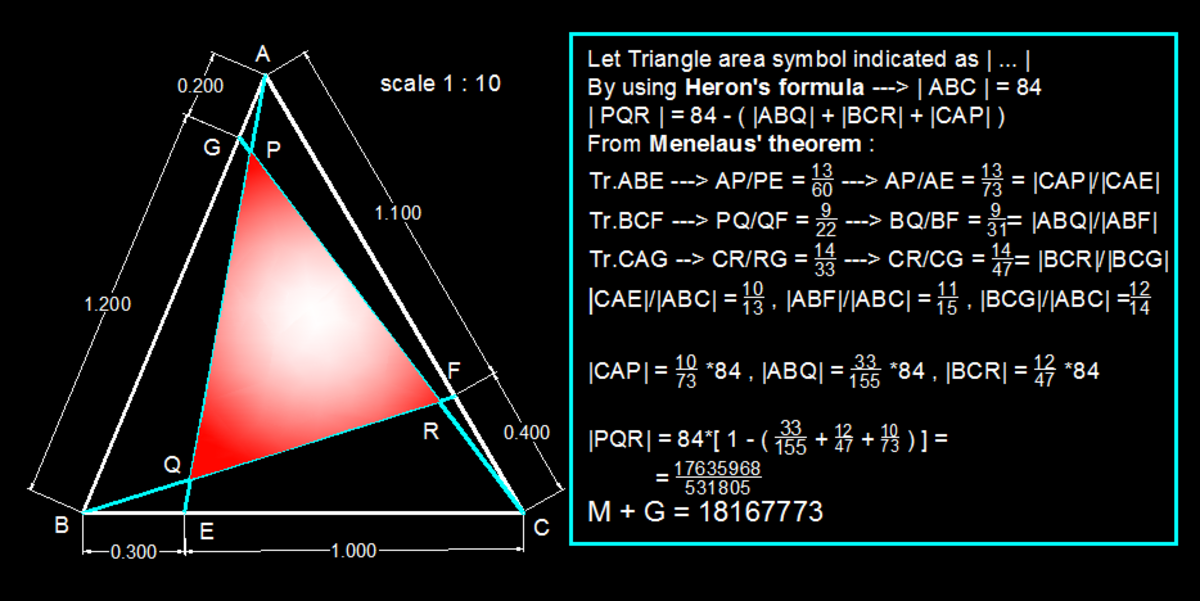
Nice solution...but can we solve it by any other method?and can you please elaborate that how by menelaus' theorem AP/PE=13/60?
Log in to reply
Menelaus' theorem,
Given a triangle ABE, and a transversal line GC that crosses AB, BE and EA at points G, C and P respectively,
then, | (AP/PE)(EC/CB)(BG/GA) | = 1
AP/PE * 10/13 * 12/2 = 1
AP/PE = 13/60
Log in to reply
Thanks and I think This is the generalised form for solving these type of problems
Good solution!
I always kept thinking a way to solve it by similarity and stuff like that, seeing no success in that I finally decided to use coordinate geometry. I assumed B = ( 0 , 0 ) and C = ( 1 3 , 0 ) . Through these two we get A = ( 1 3 7 0 , 1 3 1 6 8 ) .
Then I found out the points E , F and G . Then I found out the equations for B F , C G and A E . Then their solutions (or intersections as P , Q and R ). And then the area, of △ P Q R . I had had lost my patience till then but still I tried the answer!
The coordinates are, P = ( 9 4 9 4 7 0 7 , 9 4 9 1 0 0 8 0 ) , Q = ( 6 5 2 0 7 , 2 0 1 5 2 0 1 6 ) and R = ( 6 1 1 6 4 1 7 , 6 1 1 2 0 1 6 ) .
Very very long and tiring method.
@Harshi Singh did you used the generalized formula to solve the question in the first place?
Log in to reply
My problems are usually based on whatever i study on internet or from some similar resources , One day i was studying unknown theorem's of geometry,Thereby i came to know this theorem and thus posted a problem on it. So, yes at first place i use the formula but now Sir ahmad has shown a more delicate way to solve it........